
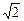 ,或k=
,或k=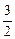 ,或k不存在时,l与C只有一个交点;当
,或k不存在时,l与C只有一个交点;当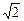 <k<
<k<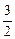 ,或-
,或-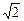 <k<
<k<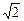 ,或k<-
,或k<-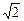 时,l与C有两个交点;当k>
时,l与C有两个交点;当k>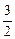 时,l与C没有交点.
时,l与C没有交点.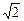 时,方程有一个根,l与C有一个交点
时,方程有一个根,l与C有一个交点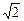 时
时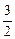 时,方程有一个实根,l与C有一个交点.
时,方程有一个实根,l与C有一个交点.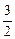 ,又k≠±
,又k≠±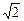 ,故当k<-
,故当k<-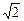 或-
或-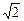 <k<
<k<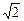 或
或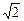 <k<
<k<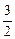 时,方程有两不等实根,l与C有两个交点.
时,方程有两不等实根,l与C有两个交点.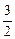 时,方程无解,l与C无交点.
时,方程无解,l与C无交点.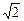 ,或k=
,或k=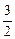 ,或k不存在时,l与C只有一个交点;
,或k不存在时,l与C只有一个交点;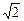 <k<
<k<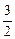 ,或-
,或-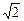 <k<
<k<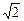 ,或k<-
,或k<-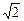 时,l与C有两个交点;
时,l与C有两个交点;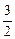 时,l与C没有交点.
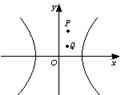
时,l与C没有交点.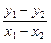 =2
=2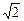 ,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在.
,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:不详 题型:单选题
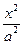 -
-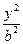 =1,点A、B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
=1,点A、B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,并且与直线y=
,并且与直线y=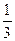 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为-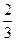 ,求这个双曲线的方程.
,求这个双曲线的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com