
(本小题满分14分)
已知函数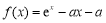 (其中
(其中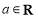 ,e是自然对数的底数,e=2.71828…).
,e是自然对数的底数,e=2.71828…).
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若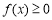 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)求证:对任意正整数n,都有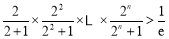 .
.
(Ⅰ)函数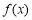 在
在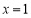 处取得极小值
处取得极小值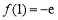 ,函数
,函数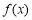 无极大值.(Ⅱ)
无极大值.(Ⅱ)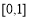 (Ⅲ)证明略
(Ⅲ)证明略
【解析】
试题分析:第一步把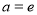 代入函数解析式,
代入函数解析式,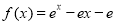 ,求极值要先求导数,
,求极值要先求导数,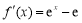 ,令
,令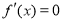 ,求出极值点
,求出极值点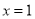 ,根据函数单调性求出极小值;第二步
,根据函数单调性求出极小值;第二步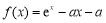 ,求导数
,求导数 ,下面针对
,下面针对 进行讨论,由于
进行讨论,由于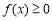 恒成立,只需
恒成立,只需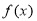 的最小值大于或等于零,最后求实数a的取值范围;
的最小值大于或等于零,最后求实数a的取值范围;
第三步依据第二步的结论,令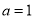 ,则
,则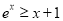 ,有
,有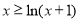 ,令
,令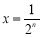 (
(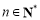 ),得
),得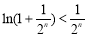 ,
,
把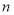 从取
从取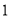 ---
---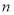 时的n个不等式相加,之后用放缩法证明出结论.
时的n个不等式相加,之后用放缩法证明出结论.
试题解析:(Ⅰ) 当 时,
时,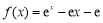 ,
,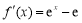 ,
,
当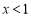 时,
时,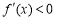 ;当
;当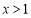 时,
时,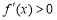 .
.
所以函数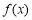 在
在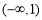 上单调递减,在
上单调递减,在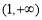 上单调递增,
上单调递增,
所以函数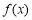 在
在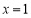 处取得极小值
处取得极小值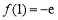 ,函数
,函数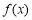 无极大值.
无极大值.
(Ⅱ)由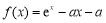 ,
, ,
,
若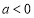 ,则
,则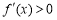 ,函数
,函数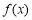 单调递增,当x趋近于负无穷大时,
单调递增,当x趋近于负无穷大时,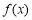 趋近于负无穷大;当x趋近于正无穷大时,
趋近于负无穷大;当x趋近于正无穷大时,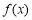 趋近于正无穷大,故函数
趋近于正无穷大,故函数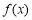 存在唯一零点
存在唯一零点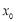 ,当
,当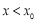 时,
时,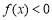 ;当
;当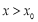 时,
时,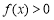 .故
.故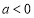 不满足条件.
不满足条件.
若 ,
,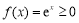 恒成立,满足条件.
恒成立,满足条件.
若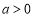 ,由
,由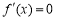 ,得
,得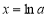 ,当
,当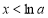 时,
时,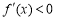 ;当
;当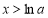 时,
时,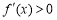 ,所以函数
,所以函数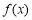 在
在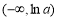 上单调递减,在
上单调递减,在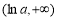 上单调递增,所以函数
上单调递增,所以函数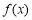 在
在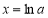 处取得极小值
处取得极小值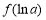
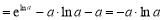 ,由
,由 得
得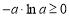 ,解得
,解得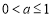 .
.
综上,满足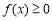 恒成立时实数a的取值范围是
恒成立时实数a的取值范围是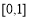 .
.
(Ⅲ)由(Ⅱ)知,当 时,
时,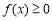 恒成立,所以
恒成立,所以 恒成立,
恒成立,
即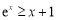 ,所以
,所以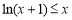 ,令
,令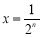 (
(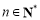 ),得
),得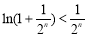 ,
,
则有
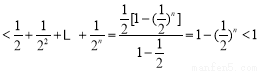 ,
,
所以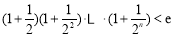 ,所以
,所以 ,即
,即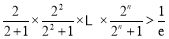 .
.
考点:1.利用导数求极值;2.利用导数导数求函数最值;3.利用导数证明不等式;本题是导数的综合应用;


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:选择题
下列五个命题:
①若xy=0,则x=0且y=0”的逆否命题;
②正方形是菱形”的否命题;
③若 ”的逆命题;
”的逆命题;
④“m>2, ”;
”;
⑤命题p:“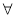
 ,
, ≥0”的否定是命题q:“
≥0”的否定是命题q:“
 ,
, ”,且命题q为假命题.
”,且命题q为假命题.
其中真命题的个数为( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数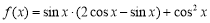 .
.
(Ⅰ)求函数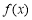 的最小正周期;
的最小正周期;
(Ⅱ)设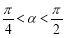 ,且
,且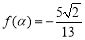 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
已知F1、F2是双曲线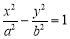 (a>0,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则该双曲线的离心率为 ( )
(a>0,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则该双曲线的离心率为 ( )
(A)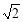 (B)
(B)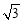
(C) 2 (D) 3
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市青浦区高三上学期期终学习质量调研数学试卷(解析版) 题型:选择题
已知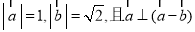 ,则向量
,则向量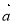 与向量
与向量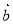 的夹角为( ).
的夹角为( ).
(A)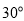 (B)
(B)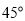 (C)
(C) 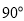 (D)
(D)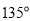
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试理科数学试卷B卷(解析版) 题型:选择题
设函数 的定义域为D,若任取
的定义域为D,若任取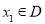 ,存在唯一的
,存在唯一的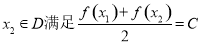 ,则称C为函数
,则称C为函数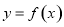 在D上的均值.给出下列五个函数:
在D上的均值.给出下列五个函数:
①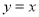 ;②
;②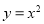 ;③
;③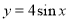 ;④
;④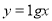 ;⑤
;⑤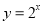 .则所有满足在其定义域上的均值为2的函数的序号为
.则所有满足在其定义域上的均值为2的函数的序号为
A.①③ B.①④ C.①④⑤ D.②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com