
| x/千元 | 50 | 70 | 80 | 40 | 30 | 90 | 95 | 97 |
| y/千件 | 100 | 80 | 60 | 120 | 135 | 55 | 50 | 48 |
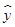 =-1.286 6x+169.772 4 (2)①128.916 2千元 ②66.477 1千元
=-1.286 6x+169.772 4 (2)①128.916 2千元 ②66.477 1千元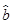 =
=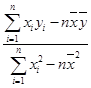 =-1.286 6,
=-1.286 6,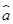 =
=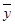 -
-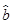
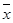 =169.772 4,
=169.772 4,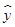 =-1.286 6x+169.772 4.
=-1.286 6x+169.772 4.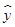 x=
x=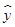 +500,
+500,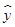 x-x=-1.286 6x2+169.772 4x+1.286 6x-169.772 4-500=-1.286 6x2+171.059x-669.772 4.
x-x=-1.286 6x2+169.772 4x+1.286 6x-169.772 4-500=-1.286 6x2+171.059x-669.772 4.

科目:高中数学 来源:不详 题型:解答题
年份 年 年 | 2009 | 2010 | 2011 | 2012 | 2013 |
平均成绩 分 分 | 97 | 98 | 103 | 108 | 109 |
 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。



查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差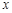 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
 关于
关于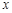 的线性回归方程
的线性回归方程 .
. ;
; .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 平均气温(℃) | -1 | 4 | 10 | 13 | 18 | 26 |
| 数量(百个) | 20 | 24 | 34 | 38 | 50 | 64 |
 =1.98x+22.13
=1.98x+22.13 =1.78x+20.13
=1.78x+20.13 =1.68x+18.73
=1.68x+18.73 =1.51x+15.73
=1.51x+15.73查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 温度(x) | 0 | 10 | 20 | 50 | 70 |
| 溶解度(y) | 66.7 | 76.0 | 85.0 | 112.3 | 128.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
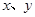 的取值如下表:
的取值如下表: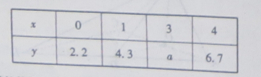
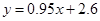 ,则表中的数据a的值为( )
,则表中的数据a的值为( )| A.4.6 | B.4.8 | C.5.45 | D.5.55 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 喜爱打篮球 | 不喜爱打篮球 | 总计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 总计 | 30 | 20 | 50 |

| P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com