
分析 由于a+b=2,b>0,从而$\frac{1}{8|a|}$+$\frac{|a|}{b}$=$\frac{1}{8|a|}$+$\frac{|a|}{2-a}$,(a<2),设f(a)=$\frac{1}{8|a|}$+$\frac{|a|}{2-a}$,(a<2),画出此函数的图象,结合导数研究其单调性,即可得出答案.
解答 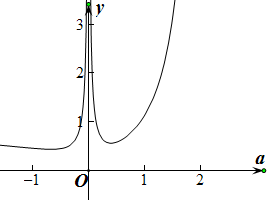 解:∵a+b=2,b>0,
解:∵a+b=2,b>0,
∴$\frac{1}{8|a|}$+$\frac{|a|}{b}$=$\frac{1}{8|a|}$+$\frac{|a|}{2-a}$,(a<2)
设f(a)=$\frac{1}{8|a|}$+$\frac{|a|}{2-a}$,(a<2),画出此函数的图象,如图所示.
利用导数研究其单调性得,
当a<0时,f(a)=-$\frac{1}{8a}$+$\frac{a}{a-2}$,
f′(a)=$\frac{1}{8{a}^{2}}$-$\frac{2}{(a-2)^{2}}$=$\frac{(5a-2)(-3a-2)}{8{a}^{2}(a-2)^{2}}$,当a<-$\frac{2}{3}$时,f′(a)<0,当-$\frac{2}{3}$<a<0时,f′(a)>0,
故函数在(-∞,-$\frac{2}{3}$)上是减函数,在(-$\frac{2}{3}$,0)上是增函数,
∴当a=-$\frac{2}{3}$时,取得最小值$\frac{5}{16}$.
同样地,当0<a<2时,得到当a=$\frac{2}{5}$时,取得最小值$\frac{7}{16}$.
综合,则当a=-$\frac{2}{3}$时,$\frac{1}{8|a|}$+$\frac{|a|}{b}$取得最小值.
故答案为:-$\frac{2}{3}$
点评 本题考查导数在最值问题的应用,考查数形结合思想,属于中档题.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[{-1,-\frac{3}{4}})$ | C. | $({\frac{3}{4},1}]$ | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | ||
| C. | 若m∥n,m∥α,n?α,则n∥α | D. | 若m∥α,α∥β,则m∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com