
| A. | [1,+∞) | B. | $[{-1,-\frac{3}{4}})$ | C. | $({\frac{3}{4},1}]$ | D. | (-∞,-1] |
分析 由直线方程的特点得到此直线恒过A(2,4),由曲线方程的特点得到曲线为一个半圆,在平面直角坐标系中画出相应的图形,根据直线与半圆有2个交点,取两个特殊情况:当直线与半圆相切,且切点在第二象限时,可得出圆心到直线的距离等于圆的半径,即d=r,利用点到直线的距离公式列出关于k的方程,求出方程的解得到此时k的值;当直线过点C时,将C的坐标代入直线方程,得到关于k的方程,求出方程的解得到此时k的值,由图象可得出满足题意k的取值范围.
解答 解:直线y=k(x-2)+4,
当x=2时,y=4,可得此直线恒过A(2,4),
曲线y=$\sqrt{4-{x^2}}$为圆心在坐标原点,半径为2的半圆,
根据题意作出相应的图形,如图所示:
当直线y=k(x-2)+4与半圆相切(切点在第二象限)时,圆心到直线的距离d=r,
∴$\frac{|4-2k|}{\sqrt{1+{k}^{2}}}$=2,即4k2-16k+16=4+4k2,
解得:k=$\frac{3}{4}$,
当直线y=k(x-2)+4过点C时,将x=-2,y=0代入直线方程得:-4k+4=0,
解得:k=1,
则直线与曲线有2个交点时k的范围为($\frac{3}{4}$,1].
故选C.
点评 此题考查了直线与圆的位置关系,利用了数形结合的数学思想,直线与圆的位置关系由d与r的大小来判断(d为圆心到直线的距离,r为圆的半径),当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
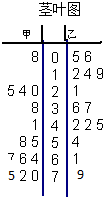 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得如图所示的统计图,根据统计图:
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得如图所示的统计图,根据统计图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,\frac{1}{3})$ | B. | $(-∞,\frac{1}{3})$ | C. | (-∞,-1) | D. | $(-\frac{1}{3},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com