
| A. | $(-1,\frac{1}{3})$ | B. | $(-∞,\frac{1}{3})$ | C. | (-∞,-1) | D. | $(-\frac{1}{3},1)$ |
分析 由已知可得,函数f(x)为偶函数,且在x≥0时为增函数,在x≤0时为减函数,若f(2x)<f(1-x),则|2x|<|1-x|,解得答案.
解答 解:∵函数数f(x)=e1+|x|-$\frac{1}{{1+{x^4}}}$,满足f(-x)=f(x),
故函数f(x)为偶函数,
当x≥0时,y=e1+|x|=e1+x为增函数,y=$\frac{1}{{1+{x^4}}}$为减函数,
故函数f(x)在x≥0时为增函数,在x≤0时为减函数,
若f(2x)<f(1-x),则|2x|<|1-x|,
即4x2<x2-2x+1,即3x2+2x-1<0,
解得:x∈(-1,$\frac{1}{3}$),
故选:A
点评 本题考查的知识点是函数单调性,函数的奇偶性,绝对值不等式的解法,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
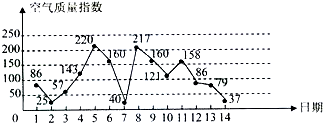 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[{-1,-\frac{3}{4}})$ | C. | $({\frac{3}{4},1}]$ | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | ||
| C. | 若m∥n,m∥α,n?α,则n∥α | D. | 若m∥α,α∥β,则m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com