
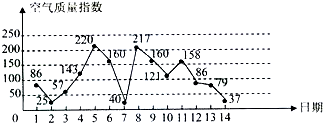
 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.分析 (Ⅰ)设“此人到达当日空气重度污染”为事件A,由于此人随机选择某一天到达该市且停留2天,从而他必须在3月1日到13日的某一天到达该城市,由折线图知:3月1日到13日有职有2天属于重度污染,由此能求出此人到达当日空气重度污染的概率.
(Ⅱ)由折线图判断从3月5日开始连续三天的空气质量指数波动最大,由此能求出结果.
(Ⅲ)依题意,X的可能取值是0,1,2,由折线图知:3月1日至14日属于优良天气的共有7天,由此能求出X的分布列和EX.
解答 解:(Ⅰ)设“此人到达当日空气重度污染”为事件A,
由于此人随机选择某一天到达该市且停留2天,
∴他必须在3月1日到13日的某一天到达该城市,
由折线图知:3月1日到13日有职有2天属于重度污染,
∴此人到达当日空气重度污染的概率P=$\frac{2}{13}$.
(Ⅱ)由折线图判断从3月5日开始连续三天的空气质量指数波动最大,
∴从3月5日开始连续三天的空气指数方差最大.
(Ⅲ)依题意,X的可能取值是0,1,2,由折线图知:
3月1日至14日属于优良天气的共有7天,
∴P(X=0)=$\frac{5}{13}$,P(X=1)=$\frac{4}{13}$,P(X=2)=$\frac{4}{13}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{5}{13}$ | $\frac{4}{13}$ | $\frac{4}{13}$ |
点评 本题考查概率的求法,考查方差的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意折线图的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20}{17}$ | B. | $\frac{38}{29}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,\frac{1}{3})$ | B. | $(-∞,\frac{1}{3})$ | C. | (-∞,-1) | D. | $(-\frac{1}{3},1)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com