
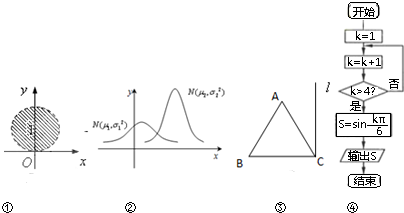
分析 (1)直接由图形可得阴影边界所对应圆的方程,再用集合表示阴影区域判断(1);(2)从正态曲线关于直线x=μ对称,看μ的大小,从曲线越“矮胖”,表示总体越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中判断(2);对于(3),几何体为圆台减去一个小圆锥,分别求出圆台和圆锥的体积判断;对于(4),读取框图,求出S的值加以判断.
解答 解:(1)图①中的阴影部分是圆x2+y2-2y=0及其内部的点,可用集合{(x,y)|x2+y2-2y<0}表示,故(1)正确;
(2)从正态曲线的对称轴的位置看,显然μ1<μ2,正态曲线越“瘦高”,表示取值越集中,σ越小.∴σ1>σ2,故(2)错误;
(3)则将△ABC绕l旋转一周得到的几何体为圆台挖去一个小圆锥,圆台的上下底面半径分别为r=1,R=2,圆台的高为h=$\sqrt{3}$.
圆锥的底面半径为r′=1,高为h=$\sqrt{3}$.∴圆台的上底面积为S=πr2=π,下底面积为S′=πR2=4π,圆锥的底面积为π,
∴圆台的体积V1=$\frac{1}{3}$(π+4π+2π)•$\sqrt{3}$=$\frac{7}{3}\sqrt{3}π$,圆锥的体积V2=$\frac{1}{3}$•π•$\sqrt{3}$=$\frac{\sqrt{3}}{3}$π.
∴几何体的体积V=V1-V2=2$\sqrt{3}$π,故(3)正确;
对于(4),给k赋值1,执行k=1+1=2,判断2>4不成立,执行k=2+1=3,判断3>4不成立,执行k=3+1=4,判断4>4不成立,执行k=4+1=5,
判断5>4成立,执行S=sin$\frac{5π}{6}$=$\frac{1}{2}$,输出S的值是$\frac{1}{2}$,是否结束,故(4)错误.
故答案为:(1)(3).
点评 本题考查命题的真假判断与应用,考查了数形结合的解题思想方法,是中档题.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
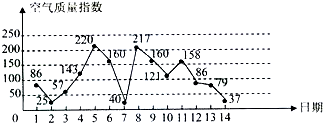 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并于第二天离开.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com