
分析 (I)利用垂径定理和勾股定理列方程解出p即可得出抛物线方程;
(II)联立方程组,由根与系数的关系得出A,B纵坐标的关系,假设存在符合条件的P点,则kPA+kPB=0,代入斜率公式化简即可求出x0,y0.
解答 解:(I)设抛物线的准线方程为x=-$\frac{p}{2}$.圆O的半径r=2,
由垂径定理得$\frac{{p}^{2}}{4}+(\frac{2\sqrt{3}}{2})^{2}$=4,解得p=2.
∴抛物线方程为y2=4x.
(II)联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=-x+m}\end{array}\right.$得y2+4y-4m=0,
∴△=16+16m>0,解得m>-1.
设A(x1,y1),B(x2,y2),则y1+y2=-4,y1y2=-4m.
若抛物线上存在定点P(x0,y0),使得直线PA,PB关于x=x0对称,
则kPA+kPB=0,
∴$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$+$\frac{{y}_{0}-{y}_{2}}{{x}_{0}-{x}_{2}}$=$\frac{{y}_{0}-{y}_{1}}{\frac{{{y}_{0}}^{2}}{4}-\frac{{{y}_{1}}^{2}}{4}}$+$\frac{{y}_{0}-{y}_{2}}{\frac{{{y}_{0}}^{2}}{4}-\frac{{{y}_{2}}^{2}}{4}}$=$\frac{4}{{y}_{0}+{y}_{1}}+\frac{4}{{y}_{0}+{y}_{2}}$=0,
∴y0=-$\frac{{y}_{1}+{y}_{2}}{2}$=2,x0=$\frac{{{y}_{0}}^{2}}{4}$=1.
∴存在点P(1,2),只要m>-1,直线PA,PB关于直线x=1对称.
点评 本题考查了抛物线的性质,直线的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
阅读如下程序框图,如果输出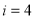 ,那么空白的判断框中应填入的条件是( )
,那么空白的判断框中应填入的条件是( )

A. B.
B.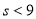 C.
C.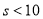 D.
D.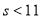
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{3}{4}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\sqrt{3}π$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com