
分析 (Ⅰ)f′(x)=$\frac{1}{x}$-a,(x>0).对a分类讨论:a≤0,a>0,利用导数研究函数的单调性;
(Ⅱ)(ⅰ)由(Ⅰ)可知,当a≤0时f(x)单调,不存在两个零点;当a>0时,可求得f(x)有唯一极大值,令其大于零,可得a的范围,再判断极大值点左右两侧附近的函数值小于零即可;(ⅱ)构造函数G(x)=h($\frac{2}{a}$-x)-h(x)=ln($\frac{2}{a}$-x)-a($\frac{2}{a}$-x)-(lnx-ax),(0<x≤$\frac{1}{a}$),根据函数的单调性证明即可.
解答 解:(Ⅰ)h′(x)=$\frac{1}{x}$-a,(x>0).
当a≤0时,h′(x)>0,函数h(x)在(0,+∞)单调递增;
当a>0时,h′(x)=$\frac{-a(x-\frac{1}{a})}{x}$,
令h′(x)>0,解得0<x<$\frac{1}{a}$;令h′(x)<0,解得x>$\frac{1}{a}$.
∴函数h(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减为($\frac{1}{a}$,+∞).
综上可得:当a≤0时,函数h(x)在(0,+∞)单调递增;
当a>0时,函数h(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减为($\frac{1}{a}$,+∞).
(Ⅱ)(ⅰ)函数f(x)与g(x)有两个不同的交点A(x1,y1)、B(x2,y2),其中x1<x2.
等价于函数h(x)有两个不同的零点x1,x2,其中x1<x2.
由(Ⅰ)知,当a≤0时,函数h(x)在(0,+∞)上是增函数,不可能有两个零点,
当a>0时,h(x)在(0,$\frac{1}{a}$)上是增函数,在($\frac{1}{a}$,+∞)上是减函数,此时h($\frac{1}{a}$)为函数f(x)的最大值,
当h($\frac{1}{a}$)≤0时,h(x)最多有一个零点,∴h($\frac{1}{a}$)=ln$\frac{1}{a}$>0,解得0<a<1,
此时,$\frac{1}{e}$<$\frac{1}{a}$<$\frac{{e}^{2}}{{a}^{2}}$,且h($\frac{1}{e}$)=-1-$\frac{a}{e}$+1=-$\frac{a}{e}$<0,
h($\frac{{e}^{2}}{{a}^{2}}$)=2-2lna-$\frac{{e}^{2}}{a}$+1=3-2lna-$\frac{{e}^{2}}{a}$(0<a<1),
令F(a)=3-2lna-$\frac{{e}^{2}}{a}$,则F'(x)=-$\frac{2}{a}$+$\frac{{e}^{2}}{{a}^{2}}$=$\frac{{e}^{2}-2a}{{a}^{2}}$>0,
∴F(a)在(0,1)上单调递增,
∴F(a)<F(1)=3-e2<0,即h($\frac{{e}^{2}}{{a}^{2}}$)<0,
∴a的取值范围是(0,1).
(ii)∵h(x)=lnx-ax+1在(0,$\frac{1}{a}$)上是增函数,在($\frac{1}{a}$,+∞)上是减函数,
∴h($\frac{1}{e}$)=-1-$\frac{a}{e}$+1=-$\frac{a}{e}$<0,h(1)=1-a>0,
故$\frac{1}{e}$<x1<1,即-1<f(x1)<0,∴-1<y1<0,
构造函数G(x)=h($\frac{2}{a}$-x)-h(x)=ln($\frac{2}{a}$-x)-a($\frac{2}{a}$-x)-(lnx-ax),(0<x≤$\frac{1}{a}$),
则G′(x)=$\frac{2{a(x-\frac{1}{a})}^{2}}{x(x-\frac{2}{a})}$<0,∴G(x)在(0,$\frac{1}{a}$]递减,
∵0<x1<$\frac{1}{a}$,∴G(x1)>G($\frac{1}{a}$)=0,
∵h(x1)=0,
∴h($\frac{2}{a}$-x1)=ln($\frac{2}{a}$-x1)-a($\frac{2}{a}$-x1)+1-h(x1)=G(x1)>0=h)x2),
∴由(Ⅰ)得:x2>$\frac{2}{a}$-x1,即${e}^{{y}_{1}}$+${e}^{{y}_{2}}$>$\frac{2}{a}$>2,
∴e${\;}^{{y}_{1}}$+e${\;}^{{y}_{2}}$>2.
点评 本题考查利用导数研究函数的单调性、零点及不等式的证明等知识,考查学生综合运用知识分析解决问题的能力、推理论证能力,本题综合性强,能力要求较高.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
已知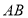 是圆
是圆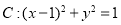 的直径,点
的直径,点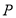 为直线
为直线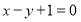 上任意一点,则
上任意一点,则
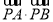 的最小值是( )
的最小值是( )
A.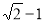 B.
B.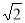 C.
C. 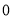 D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
已知函数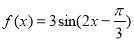 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.导函数为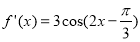
B.函数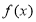 的图象关于直线
的图象关于直线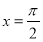 对称
对称
C.函数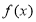 在区间
在区间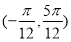 上是增函数
上是增函数
D.函数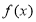 的图象可由函数
的图象可由函数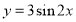 的图象向右平移
的图象向右平移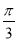 个单位长度得到
个单位长度得到
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com