
分析 (1)求导数,f′(x)=[ax2+(2a+1)x+1]•ex,可设g(x)=ax2+(2a+1)x+1,要找f(x)的单调递增区间,只要找使g(x)≥0的区间即可,这样可讨论a:a=0时,g(x)=x+1,从而得出f(x)的单调递增区间为[-1,+∞),而a≠0时,可找使得二次函数g(x)≥0的区间即可;
(2)由题意便知,要存在这样的x1,需让f(x)在(0,2)上的值域包含g(x)在(0,2)上的值域,从而根据导数符号,分别求出g(x),f(x)在(0,2)上的值域,然后判断是否满足包含关系即可.
解答 解:(1)f′(x)=[ax2+(2a+1)x+1]•ex,设g(x)=ax2+(2a+1)x+1;
①若a=0,则g(x)=x+1;
∴x≥-1时,f′(x)≥0;
∴f(x)的单调递增区间为:[-1,+∞);
②若a≠0,解g(x)=0得,$x=\frac{-(2a+1)±\sqrt{4{a}^{2}+1}}{2a}$;
1)a>0时,x$≤\frac{-(2a+1)-\sqrt{4{a}^{2}+1}}{2a}$,或$x≥\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}$时,g(x)≥0,∴f′(x)≥0;
∴f(x)的单调递增区间为:$(-∞,\frac{-(2a+1)-\sqrt{4{a}^{2}+1}}{2a}]$,[$\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}$,+∞);
2)a<0时,$\frac{-(2a+1)-\sqrt{4{a}^{2}+1}}{2a}$$≤x≤\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}$时,g(x)≥0,∴f′(x)≥0;
∴f(x)的单调递增区间为:[$\frac{-(2a+1)-\sqrt{4{a}^{2}+1}}{2a},\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}$];
(2)根据题意知,f(x)在(0,2)上的值域包含g(x)在(0,2)上的值域;
g′(x)=$\frac{1-2{x}^{2}}{2x}$;
∴$0<x<\frac{1}{\sqrt{2}}$时,g′(x)>0,$\frac{1}{\sqrt{2}}<x<2$时,g′(x)<0;
∴$x=\frac{1}{\sqrt{2}}$时,g(x)取最大值$-\frac{1}{4}-\frac{1}{4}ln2+{e}^{2}$,而x趋向0时,g(x)趋向-∞;
∴g(x)在(0,2)上的值域为(-∞,$-\frac{1}{4}-\frac{1}{4}ln2+{e}^{2}$];
①当$-\frac{3}{8}<a<0$时,$\frac{-(2a+1)-\sqrt{4{a}^{2}+1}}{2a}<0$,$0<\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}<2$;
∴由①知,$0<x<\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}$时,f′(x)>0,$\frac{-(2a+1)+\sqrt{4{a}^{2}+1}}{2a}<x<2$时,f′(x)<0;
而x趋向0或2时,f(x)都不趋向于负无穷;
∴不满足f(x)在(0,2)上的值域包含g(x)在(0,2)上的值域;
②当a=0时,由(1)知f(x)在(0,2)上单调递增;
∴f(x)的值域为(0,2e2),不满足条件;
③当a>0时,$\frac{-(2a+1)±\sqrt{4{a}^{2}+1}}{2a}<0$;
∴f(x)在(0,2)上单调递增;
∴f(x)的值域为(0,(4a+2)e2),不满足条件;
∴综上得,不存在x1∈(0,2),使得任意x2∈(0,2),有f(x1)=g(x2).
点评 考查根据导数符号找函数单调区间的方法,二次函数的符号和对应一元二次方程实数根的关系,解一元二次方程,根据导数求函数最值的方法,以及根据导数求函数值域的方法和过程,注意不要漏了a=0的情况.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | c≥4 | B. | c≥3 | C. | c≥2 | D. | c≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
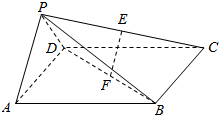 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{4}{3}$) | B. | (2,$\frac{2}{3}$) | C. | (-1,$\frac{2}{3}$) | D. | (-2,-$\frac{14}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com