
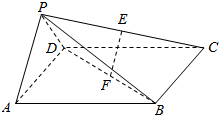
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.分析 (1)可取AD中点O,BC中点G,并连接PO,OG,根据已知条件即可说明OA,OG,OP三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,可设PA=1,从而可确定图形上一些点的坐标,从而可求出$\overrightarrow{EF},\overrightarrow{PA}$的坐标,根据共线向量基本定理即可说明$\overrightarrow{EF}$∥$\overrightarrow{PA}$,从而得出EF∥PA,根据线面平行的判定定理即可得出EF∥平面PAD;
(2)根据已知条件可得到PA⊥PD,并且有CD⊥平面PAD,从而根据线面垂直及面面垂直的判定定理即可得出平面PAB⊥平面PDC;
(3)可说明$\overrightarrow{PA}$为平面PCD的法向量,并设直线BD与平面PCD所成角的大小为θ,然后根据$sinθ=|cos<\overrightarrow{PA},\overrightarrow{BD}>|$即可求出sinθ,从而得出θ.
解答 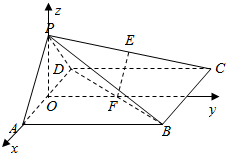 解:(1)证明:如图,取AD中点O,BC中点G,连接PO,OG,PA=PD,∴PO⊥AD;
解:(1)证明:如图,取AD中点O,BC中点G,连接PO,OG,PA=PD,∴PO⊥AD;
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,PO?侧面PAD;
∴PO⊥底面ABCD,又ABCD为正方形,O,G分别为AD,BC中点;
∴OA,OG,OP三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,设PA=1,则根据条件可确定以下几点坐标:
O(0,0,0),A($\frac{\sqrt{2}}{2}$,0,0),$B(\frac{\sqrt{2}}{2},\sqrt{2},0)$,$C(-\frac{\sqrt{2}}{2},\sqrt{2},0)$,D($-\frac{\sqrt{2}}{2}$,0,0),P(0,0,$\frac{\sqrt{2}}{2}$),E($-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4}$),F(0,$\frac{\sqrt{2}}{2}$,0);
∴$\overrightarrow{EF}=(\frac{\sqrt{2}}{4},0,-\frac{\sqrt{2}}{4})$,$\overrightarrow{PA}=(\frac{\sqrt{2}}{2},0,-\frac{\sqrt{2}}{2})$;
∴$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{PA}$;
∴$\overrightarrow{EF}$∥$\overrightarrow{PA}$;
∴EF∥PA,PA?平面PAD,EF?平面PAD;
∴EF∥平面PAD;
(2)根据PA=PD=$\frac{\sqrt{2}}{2}AD$便得,∠APD=90°,即PA⊥PD;
又CD⊥平面PAD,PA?平面PAD;
∴CD⊥PA,即PA⊥CD,PD∩CD=D;
∴PA⊥平面PDC,PA?平面PAB;
∴平面PAB⊥平面PDC;
(3)根据(2)PA⊥平面PCD;
∴$\overrightarrow{PA}=(\frac{\sqrt{2}}{2},0,-\frac{\sqrt{2}}{2})$为平面PCD的法向量,$\overrightarrow{BD}$=($-\sqrt{2},-\sqrt{2},0$);
设直线BD与平面PCD所成角为θ,则sinθ=$|cos<\overrightarrow{PA},\overrightarrow{BD}>|$=$\frac{1}{1•2}=\frac{1}{2}$;
∴θ=30°;
∴直线BD和平面PCD所成角的大小为30°.
点评 考查建立空间直角坐标系,利用空间向量解决立体几何问题的方法,面面垂直的性质定理,线面垂直、面面垂直的判定定理,以及共线向量基本定理,线面平行的判定定理,平面法向量的概念,向量夹角的余弦公式.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-3,-1) | C. | (-1,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0|0<x<2} | B. | {x|0<x<$\sqrt{6}$} | C. | {x|0<x<2.5} | D. | {x|0<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com