
分析 由直线的方程可得直线的斜率,进而可得tanα∈[-$\sqrt{3}$,$\sqrt{3}$],由正切函数的性质可得.
解答 解:直线3cosθ•x+$\sqrt{3}$y-a=0的斜率k=-$\frac{3cosθ}{\sqrt{3}}$=-$\sqrt{3}$cosθ∈[-$\sqrt{3}$,$\sqrt{3}$],
设直线的倾斜角为α,则tanα∈[-$\sqrt{3}$,$\sqrt{3}$],
由正切函数的性质可得0≤α≤$\frac{π}{3}$或$\frac{2π}{3}$≤α<π
故答案为:0≤α≤$\frac{π}{3}$或$\frac{2π}{3}$≤α<π
点评 本题考查直线的倾斜角,涉及正切函数的性质,属中档题.


科目:高中数学 来源: 题型:解答题
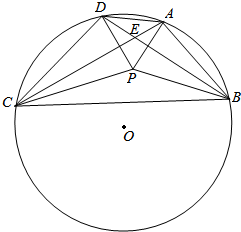 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-3,-1) | C. | (-1,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四面体ABCS中,SA,SB,SC两两垂直,∠ABS=45°,∠ABC=60°,M为AB的中点.
如图,四面体ABCS中,SA,SB,SC两两垂直,∠ABS=45°,∠ABC=60°,M为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com