
 =f(e)=e
=f(e)=e -e-1.
-e-1. 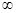 ,1)
,1) -x-lnx,f′(x)=2x-1-
-x-lnx,f′(x)=2x-1- =
= >0,
>0, =f(e)=e
=f(e)=e -e-1. 4分
-e-1. 4分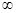 ). 由f(x)>0,得|x-a|>
). 由f(x)>0,得|x-a|> . *
. * <0,不等式*恒成立,
<0,不等式*恒成立, =0,所以a
=0,所以a 1; 6分
1; 6分 恒成立或a>x+
恒成立或a>x+ 恒成立.
恒成立. ,则h′(x)=
,则h′(x)=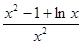 .
. 恒成立等价于a<(h(x))
恒成立等价于a<(h(x))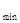 ,所以a≤1.
,所以a≤1. ,则g′(x)=
,则g′(x)=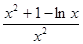 .再令e(x)=x
.再令e(x)=x +1-lnx,则e′(x)=2x-
+1-lnx,则e′(x)=2x- >0在x∈(1,+
>0在x∈(1,+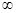 )上恒成立,e(x)在x∈(1,+
)上恒成立,e(x)在x∈(1,+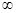 )上无最大值. 11分
)上无最大值. 11分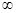 ,1). 12分
,1). 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com