Question

1．已知点P是正方体ABCD-A₁B₁C₁D₁表面上一动点，且满足|PA|=2|PB|，设PD₁与平面ABCD所成的角为θ，则θ的最大值是$\frac{π}{4}$．

Answer 1

分析 先求出点P的轨迹方程，再利用正方体的几何性质解决找出θ取得最大值时P点的位置，求出θ的最大值．

解答 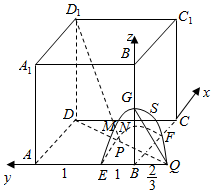解：以B为原点，分别以BC，BA，BB₁为x、y、z轴建立空间直角坐标系，
设P（x，y，z），A（0，2，0），
∵|PA|=2|PB|，
∴$\sqrt{{x}^{2}+（y-2）^{2}+{z}^{2}}$=2$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$，化简得：x²+（y+$\frac{2}{3}$）²+z²=$\frac{16}{9}$．，
∴点P的轨迹为以点Q（0，-$\frac{2}{3}$，0）为球心，以$\frac{4}{3}$为半径的球与正方体表面的交线，即图中弧$\widehat{EMG}$，$\widehat{GSF}$，$\widehat{ENF}$，
故当PD₁与底面ABCD所成角最大，则PD₁与底面ABCD的交点R与点D的距离最短，
∴当点P为DQ与$\widehat{ENF}$的交点时，PD₁与平面ABCD所成的角θ最大．
设正方体的边长为2，则AD=2，AQ=$\frac{8}{3}$，∴DQ=$\sqrt{A{D}^{2}+A{Q}^{2}}$=$\frac{10}{3}$，∴DP=DQ-PQ=2．
∴tanθ=$\frac{D{D}_{1}}{DP}$=1，故θ最大值为$\frac{π}{4}$．
故答案为：$\frac{π}{4}$．

点评 本题考查了动点的轨迹，线面角的定义，考查空间想象能力，逻辑思维能力，属中档题．