
 如图,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点,一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于点P,Q.
如图,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点,一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于点P,Q.分析 (1)设出直线AB:y=kx+c,代入抛物线的方程,运用韦达定理和向量的数量积的坐标表示,解方程可得c的值;
(2)运用中点坐标公式可得Q的坐标,运用两点的斜率公式,可得QA的斜率,求得抛物线对应函数的导数,可得切线的斜率,即可得证;
(3)设A(t,t2),这里xA=t≠0,由(2)知过A的与y=x2有且仅有一个公共点的斜率存在的直线必为y=2tx-t2.求得Q的横坐标,P的横坐标,求得AC的方程,联立抛物线的方程,求得B的横坐标,运用中点坐标公式,即可判断P为线段AB的中点.
解答 解:(1)设直线AB:y=kx+c,与y=x2联立,得x2-kx-c=0,
设A(x1,y1),B(x2,y2),
则x1x2=-c,从而y1y2=x12x22=c2,
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=2,可得c2-c=2得c=2或-1(舍去),
得c=2;
(2)证明:由(1)可得$\frac{{{x_1}+{x_2}}}{2}=\frac{k}{2}$,
故直线PQ:x=$\frac{k}{2}$,可得Q($\frac{k}{2}$,-1).
设$A({x_1},x_1^2)$,kQA=$\frac{{{x}_{1}}^{2}+1}{{x}_{1}-\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{2({{x}_{1}}^{2}+1)}{{x}_{1}-{x}_{2}}$,
由(1)可得x1x2=-1,即有x2=-$\frac{1}{{x}_{1}}$,
可得kQA=$\frac{2({{x}_{1}}^{2}+1)}{{x}_{1}-(-\frac{1}{{x}_{1}})}$=2x1,
由y=x2的导数为y′=2x,
可得过A的切线的斜率为2x1,
故直线QA与该抛物线有且仅有一个公共点;
(3)设A(t,t2),这里xA=t≠0,
由(2)知过A的与y=x2有且仅有一个公共点的斜率存在的直线必为y=2tx-t2.
与y=-1相交,得xQ=$\frac{{t}^{2}-1}{2t}$,
故xP=$\frac{{t}^{2}-1}{2t}$,$\overrightarrow{CA}$=(t,t2-1),
所以直线AC:y=(t-$\frac{1}{t}$)x+1,与y=x2联立,得x2-(t-$\frac{1}{t}$)x-1=0,
即(x-t)(x+$\frac{1}{t}$)=0,故xB=-$\frac{1}{t}$.
这样${x_P}=\frac{1}{2}({x_A}+{x_B})$,即P是AB的中点.
点评 本题考查抛物线的方程和性质,直线和抛物线相切的条件,考查向量的数量积的坐标表示,以及直线的斜率公式的运用,化简整理的运算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
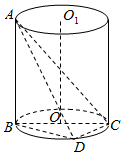 如图,AB是圆柱OO1的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,AB=5,BC=5,CD=3.
如图,AB是圆柱OO1的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,AB=5,BC=5,CD=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+3=0 | B. | 2x+y+3=0 | C. | 2x-y-3=0 | D. | 2x+y-3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com