
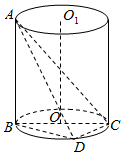
 如图,AB是圆柱OO1的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,AB=5,BC=5,CD=3.
如图,AB是圆柱OO1的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,AB=5,BC=5,CD=3.分析 (1)由AB⊥CD,BD⊥CD得出CD⊥平面ABD,故而∠CAD即为所求角,利用勾股定理得出AC,即可得出sin∠CAD;
(2)过B作BM⊥AD,垂足为M,通过证明平面ABD⊥平面ACD得出BM⊥平面ACD,利用等面积法求出BM;
(3)△ACD绕AB旋转而成的封闭几何体为大圆锥中挖去一个小圆锥,使用作差法求出体积.
解答 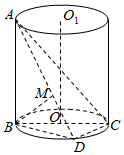 解:(1)∵AB⊥平面BCD,CD?平面BCD,
解:(1)∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD,
∵BC是圆O的直径,
∴BD⊥CD,
又BD?平面ABD,AB?平面ABD,AB∩BDE=B,
∴CD⊥平面ABD.
∴∠CAD是AC与平面ABD所成的角.
∵AB=BC=5,∴AC=5$\sqrt{2}$,
∴sin∠CAD=$\frac{CD}{AC}$=$\frac{3\sqrt{3}}{10}$.
∴直线AC与平面ABD所成角的大小为$arcsin\frac{{3\sqrt{2}}}{10}$.
(2)过B作BM⊥AD,垂足为M,
由(1)得CD⊥平面ABD,CD?平面ACD,
∴平面ABD⊥平面ACD,
又平面ABD∩平面ACD=AD,BM?平面ABD,BM⊥AD,
∴BM⊥平面ACD.
∵BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=4,∴AD=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{41}$.
∴BM=$\frac{AB•BD}{AD}$=$\frac{20\sqrt{41}}{41}$.即B到平面ACD的距离为$\frac{{20\sqrt{41}}}{41}$.
(3)线段AC绕AB旋转一周所得几何体为以BC为底面半径,以AB为高的圆锥,
线段AD绕AB旋转一周所得几何体为以BD为底面半径,以AB为高的圆锥,
∴△ACD绕AB旋转一周而成的封闭几何体的体积V=$\frac{1}{3}πB{C}^{2}•AB$-$\frac{1}{3}πB{D}^{2}•AB$=15π.
点评 本题考查了线面垂直的判定,空间角的计算,旋转体的体积计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
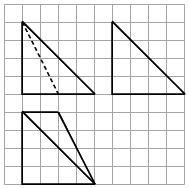 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | -1 | 0 | 1 | 2 | 3 |
| P | 0.16 | $\frac{a}{10}$ | a2 | $\frac{a}{5}$ | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点,一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于点P,Q.
如图,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点,一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com