
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|x<-1} | D. | {x|x>-1} |
分析 根据条件构造函数g(x)=f(x)-$\frac{x}{2}$-$\frac{1}{2}$,然后利用导数研究函数的单调性和最值即可得到结论.
解答 解:设g(x)=f(x)-$\frac{x}{2}$-$\frac{1}{2}$,
则g'(x)=f'(x)-$\frac{1}{2}$,
∵f(x)的导函数f′(x)≥$\frac{1}{2}$,
∴g'(x))=f'(x)-$\frac{1}{2}≥$0,
即函数g(x)在定义域上单调递增,
∵g(1)=f(1)-$\frac{1}{2}-$$\frac{1}{2}$=0,
∴当x<1时,g(x)<g(1)=0,
∴不等式f(x)<$\frac{x}{2}$+$\frac{1}{2}$的解集为(-∞,1),
故选:A.
点评 本题主要考查不等式的解法,利用条件构造函数,利用导数研究函数的单调性是解决本题的关键,综合考查函数的性质.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
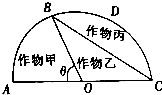 某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.
某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢运动 | 不喜欢运动 | 总计 | |
| 男 | a | b | 50 |
| 女 | c | d | 50 |
| 总计 | 30 | 70 | 100 |
| P(χ2≥k) | 0.05 | 0.001 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com