
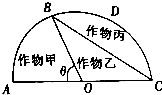
 ijũ����һ����OΪԲ�ģ�R��RΪ��������λΪ�ף�Ϊ�뾶�İ�Բ�Σ���ͼ����ֲ�أ�ũ�����ƻ�����������ã���������AOB����������ֲ����׳��ۣ���BOC����������ֲ�����ҳ��ۣ���������������ֲ����������ۣ���֪��ֲ�����������40Ԫ/ƽ���ף���ֲ�����ҵ�������80Ԫ/ƽ���ף���ֲ������ijɱ���20Ԫ/ƽ���ף�
ijũ����һ����OΪԲ�ģ�R��RΪ��������λΪ�ף�Ϊ�뾶�İ�Բ�Σ���ͼ����ֲ�أ�ũ�����ƻ�����������ã���������AOB����������ֲ����׳��ۣ���BOC����������ֲ�����ҳ��ۣ���������������ֲ����������ۣ���֪��ֲ�����������40Ԫ/ƽ���ף���ֲ�����ҵ�������80Ԫ/ƽ���ף���ֲ������ijɱ���20Ԫ/ƽ���ף����� ��1�����COD=�ȣ���λ�����ȣ����������������ȥ�����ε�����������������CMDC�����S��=f���ȣ���
��2����������ΪW���ȣ�Ԫ����������40Ԫ/ƽ���ף���ֲ�����ҵ�������80Ԫ/ƽ���ף���ֲ������ijɱ���20Ԫ/ƽ���ף����õ���ȷ�����������ֵ���õ������
��� �⣺��1�������ε������ʽ$s=\frac{1}{2}•��{•r}^{2}$�ɵã�${S}_{A0B}=\frac{1}{2}•��•{R}^{2}$��
��������$s=\frac{1}{2}absinx$���ɵã�${S}_{OBC}=\frac{1}{2}{R}^{2}sin����-�ȣ�$
��${S}_{BCD}=\frac{��}{2}{R}^{2}-\frac{1}{2}��{R}^{2}-\frac{1}{2}{R}^{2}sin����-�ȣ�$��
����$f���ȣ�=\frac{1}{2}{R}^{2}����-��-sin�ȣ�$
��2����������ΪW���ȣ�����W���ȣ�=40•SAOB+80•SOBC-20•SBCD
��W���ȣ�=30R2��+50R2Sin��-10R2��
W���ȣ�'=30R2+50R2cos��
��W���ȣ�'=0�����$cos��=-\frac{3}{5}$����$cos�ȣ�-\frac{3}{5}$ʱ��W���ȣ�'��0��
��$cos�ȣ�-\frac{3}{5}$ʱ��W���ȣ�'��0��
��W���ȣ���$cos��=-\frac{3}{5}$�������ֵ��
��������Ϊw���ʱ��$cos��=-\frac{3}{5}$��
�����ҵ���ֲ���${S}_{OBC}=\frac{1}{2}{R}^{2}sin����-�ȣ�$=$\frac{1}{2}$R2•sin��
��0���ȣ��У�$cos��=-\frac{3}{5}$��
��sin��=$\frac{4}{5}$��
�ʵ��ҵ���ֲ���Ϊ$\frac{1}{2}$R2•sin��=$\frac{2}{5}{R}^{2}$��
���� ���⿼�������Ǻ�����ʵ�������е�Ӧ�ã����Ǻ����Ļ����������ã�����������ת��˼�룻�����е��⣮


 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=1 | B�� | x=-1 | C�� | x=$\frac{1}{2}$ | D�� | x=-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��b��a | C�� | a��c��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��1} | B�� | {x|x��1} | C�� | {x|x��-1} | D�� | {x|x��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2cos240��-1 | B�� | 2sin6��cos6�� | ||
| C�� | sin50��cos37��-sin40��cos53�� | D�� | $\frac{\sqrt{3}}{2}$sin41��-$\frac{1}{2}$cos41�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com