
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
分析 函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$在R上减函数,比较三个自变量的大小,可得答案.
解答 解:函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$在R上减函数,
∵${log_2}\frac{1}{3}$∈(-∞,0),${2^{\frac{1}{3}}}$∈(1,+∞),${3^{-\frac{1}{2}}}$∈(0,1),
∴a>c>b,
故选:C.
点评 本题考查的知识点是分段函数的应用,函数的单调性,指数函数和对数函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
| 学习雷锋精神前 | 50 | 150 | 200 |
| 学习雷锋精神后 | 30 | 170 | 200 |
| 总 计 | 80 | 320 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
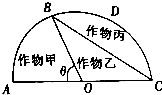 某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.
某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,3} | C. | {1,4} | D. | {1,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com