
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
分析 当a=0时,函数f(x)=2x2-1有且只有两个零点,满足条件;当a≠0时,函数的极值为0,进而得到答案.
解答 解:当a=0时,函数f(x)=2x2-1有且只有两个零点,满足条件;
当a≠0时,令f′(x)=3ax2+4x=0,解得:x=0,或x=-$\frac{4}{3a}$,
∵f(0)=1≠0,
∴f(-$\frac{4}{3a}$)=$\frac{32}{27{a}^{2}}-1=0$,
解得:a=$±\frac{4\sqrt{6}}{9}$,
故a∈{-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$},
故选:D
点评 本题考查的知识点是函数的零点及零点个数,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
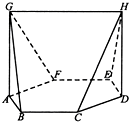 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2]∪[2,+∞) | C. | [2,+∞) | D. | a∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com