
分析 (1)函数f(x)=x|x-a|+3x=$\left\{\begin{array}{l}{x}^{2}+(3-a)x,x≥a\\-{x}^{2}+(3+a)x,x<a\end{array}\right.$,由f(x)在R上是增函数,则$\left\{\begin{array}{l}a≥\frac{a-3}{2}\\ a≤\frac{a+3}{2}\end{array}\right.$,解得实数a的取值范围;
(2)由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,进而可得满足条件的实数a的取值范围.
解答 解:(1)∵函数f(x)=x|x-a|+3x=$\left\{\begin{array}{l}{x}^{2}+(3-a)x,x≥a\\-{x}^{2}+(3+a)x,x<a\end{array}\right.$ …(2分)
由f(x)在R上是增函数,则$\left\{\begin{array}{l}a≥\frac{a-3}{2}\\ a≤\frac{a+3}{2}\end{array}\right.$…(4分)
即-3≤a≤3,
所以a的取值范围为-3≤a≤3.…(6分)
(2)由题意得对任意的实数x∈[1,2],
f(x)<g(x)恒成立,即x|x-a|<1,
即|x-a|<$\frac{1}{x}$,
即-$\frac{1}{x}$<x-a<$\frac{1}{x}$,
即x-$\frac{1}{x}$<a<x+$\frac{1}{x}$,
故只要x-$\frac{1}{x}$<a且a<x+$\frac{1}{x}$在x∈[1,2]上恒成立即可,
在x∈[1,2]时,只要x-$\frac{1}{x}$的最大值小于a且x+$\frac{1}{x}$的最小值大于a即可,…(8分)
而当x∈[1,2]时,y=x-$\frac{1}{x}$单调递增,所以x-$\frac{1}{x}$的最大值为$\frac{3}{2}$;…(11分)
当x∈[1,2]时,y=x+$\frac{1}{x}$单调递增,所以x+$\frac{1}{x}$的最小值为2…(14分)
所以$\frac{3}{2}$<a<2.…(16分)
点评 本题考查的知识点是分段函数的应用,函数的单调性,函数的最值,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
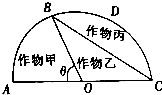 某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.
某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | -18 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com