Question

15．边长为4$\sqrt{3}$的等边△ABC中，D为边AB的中点，若P为线段CD的中点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$的值为（　　）

• A． 18
• B． -18
• C． 2$\sqrt{3}$
• D． -2$\sqrt{3}$

Answer 1

分析 可画出图形，根据条件即可求出CD=6，并且根据向量加法平行四边形法则及相反向量概念即可得到$\overrightarrow{PA}+\overrightarrow{PB}=-2\overrightarrow{PC}$，从而带入$（\overrightarrow{PA}+\overrightarrow{PB}）•\overrightarrow{PC}$进行向量数量积的运算即可求出该值的大小．

解答 解：如图，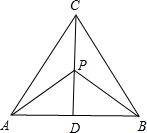

根据条件，CD=$4\sqrt{3}×\frac{\sqrt{3}}{2}$=6，CP=3，
$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PD}=-2\overrightarrow{PC}$；
∴$（\overrightarrow{PA}+\overrightarrow{PB}）•\overrightarrow{PC}=-2{\overrightarrow{PC}}^{2}=-18$．
故选B．

点评 考查等边三角形的中线也是高线，三角函数定义，以及向量加法的平行四边形法则，向量的数乘运算，向量数量积的计算公式．