
| 损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
| 学习雷锋精神前 | 50 | 150 | 200 |
| 学习雷锋精神后 | 30 | 170 | 200 |
| 总 计 | 80 | 320 | 400 |
分析 (1)求出百分比,即可判断出结论.
(2)根据独立性检验观测值的计算公式及其题中的数据计算k,进而判断出结论.
解答 解:(1)学习雷锋精神前座椅的损坏的百分比是:$\frac{50}{200}=25%$,
学习雷锋精神后座椅的损坏的百分比是:$\frac{30}{200}=15%$,
∵二者有明显的差异,∴初步判断损毁座椅减少与学习雷锋精神是否有关.
(2)根据题中的数据计算:$k=\frac{{400×{{(50×170-30×150)}^2}}}{80×320×200×200}=6.25$,
∵6.25>5.024,
∴有97.5%以上的把握认为:损毁座椅数减少与学习雷锋精神有关.
点评 本题考查了独立性检验的原理及其计算公式、百分比的计算公式,考查了推理能力与计算能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=1 | B. | x=-1 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
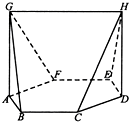 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com