练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．下列各式中，最小的是（　　）
    A．2cos240°-1B．2sin6°cos6°
    C．sin50°cos37°-sin40°cos53°D．$\frac{\sqrt{3}}{2}$sin41°-$\frac{1}{2}$cos41°

    分析 利用二倍角公式以及两角和与差的三角函数化简选项，然后找出最小者即可．

    解答 解：2cos240°-1=cos80°=sin10°；
    2sin6°cos6°=sin12°．
    sin50°cos37°-sin37°cos50°=sin13°，
    $\frac{\sqrt{3}}{2}$sin41°-$\frac{1}{2}$cos41°=sin11°．
    显然sin10°是最小的．
    故选：A．

    点评 本题考查三角函数的最值，二倍角公式与两角和与差的三角函数的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=x3-3ax-1，（a≠0）．
    （1）求f（x）的单调区间；
    （2）若f（x）在x=-1处取得极值，直线y=m与y=f（x）的图象有且只有一个交点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

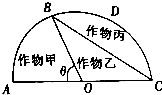    10．某农场有一块以O为圆心，R（R为常数，单位为米）为半径的半圆形（如图）种植地，农场主计划对其合理利用，其中扇形AOB区域用于种植作物甲出售，△BOC区域用于种植作物乙出售，其余区域用于种植作物丙不出售，已知种植作物甲的利润是40元/平方米；种植作物乙的利润是80元/平方米；种植作物丙的成本是20元/平方米．
    （1）设∠AOB=θ（单位：弧度，0＜θ＜π），用θ表示弓形BCD的面积f（θ）；
    （2）求总利润最大时cosθ的大小，并计算此时作物乙的种植面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知A船在灯塔C北偏东80°处，距离灯塔C为2km，B船在灯塔C北偏西40°，A、B两船的距离为3km，则∠ABC的余弦值$\frac{{\sqrt{6}}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知某校5个学生的数学和物理成绩如表
    学生的编号i12345
    数学xi8075706560
    物理yi7066686462
    （Ⅰ）假设在对这5名学生成绩进行统计时，把这5名学生的物理成绩搞乱了，数学成绩没出现问题，问：恰有2名学生的物理成绩是自己的实际分数的概率是多少？
    （Ⅱ）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系的，在上述表格是正确的前提下，用x表示数学成绩，用y表示物理成绩，求y与x的回归方程；
    参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．曲线y=$\frac{1}{x}$与y=x2在它们交点处的两条切线与x轴所围成的三角形的面积为（　　）
    A．$\frac{3}{4}$B．$\frac{3}{2}$C．1D．$\frac{3}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设集合A={x|x2-4x+3=0}，B={x|x2-5x+4=0}，集合A∪B为（　　）
    A．{1}B．{1，3}C．{1，4}D．{1，3，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知圆C：x2+y2-2x-8=0，直线l：x+ay-3a=0．
    （1）当直线l与圆C相切时，求实数a的值；
    （2）当直线l与圆C相交于A、B两点，且AB=4$\sqrt{2}$时，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下列关于算法的说法中，正确的是（　　）
    A．算法是某个问题的解决过程B．算法执行后可以不产生确定的结果
    C．解决某类问题的算法不是唯一的D．算法可以无限的操作下去不停止

    查看答案和解析>>

    同步练习册答案