
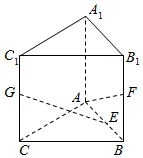
 已知三棱柱ABC-A1B1C1,侧棱AA1⊥底面ABC,AB=AC=AA1=2,∠BAC=90°,E,F分别是AB,BB1的中点,G为CC1上动点,当AF,EG所成角最小时,FG与平面AA1BB1所成角的余弦值为$\frac{\sqrt{5}}{3}$.
已知三棱柱ABC-A1B1C1,侧棱AA1⊥底面ABC,AB=AC=AA1=2,∠BAC=90°,E,F分别是AB,BB1的中点,G为CC1上动点,当AF,EG所成角最小时,FG与平面AA1BB1所成角的余弦值为$\frac{\sqrt{5}}{3}$. 分析 以A为原点,以AC,AB,AA1为坐标轴建立空间直角坐标系,设G(2,0,a),求出AF,EG所成角的余弦关于a的函数,利用导数得出此函数的极大值点为a=0,即G与C重合.然后使用定义求出线面角的余弦值.
解答 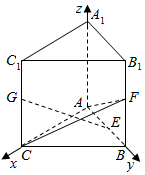 解:以A为原点,以AC,AB,AA1为坐标轴建立空间直角坐标系,如图所示:
解:以A为原点,以AC,AB,AA1为坐标轴建立空间直角坐标系,如图所示:
则A(0,0,0),E(0,1,0),F(0,2,1),设G(2,0,a),(0≤a≤2).
则$\overrightarrow{AF}$=(0,2,1),$\overrightarrow{EG}$=(2,-1,a).
∴$\overrightarrow{AF}•\overrightarrow{EG}$=a-2,|$\overrightarrow{AF}$|=$\sqrt{5}$,|$\overrightarrow{EG}$|=$\sqrt{5+{a}^{2}}$
∴cos<$\overrightarrow{AF}$,$\overrightarrow{EG}$>=$\frac{\overrightarrow{AF}•\overrightarrow{EG}}{|\overrightarrow{AF}||\overrightarrow{EG}|}$=$\frac{a-2}{\sqrt{5}•\sqrt{5+{a}^{2}}}$.
∴AF,EG所成角的余弦值为$\frac{2-a}{\sqrt{5}\sqrt{{a}^{2}+5}}$=$\frac{1}{\sqrt{5}}\sqrt{\frac{{a}^{2}-4a+4}{{a}^{2}+5}}$.
令f(a)=$\frac{{a}^{2}-4a+4}{{a}^{2}+5}$,则f′(a)=$\frac{4{a}^{2}+2a-20}{({a}^{2}+5)^{2}}$.
令f′(a)=0,解得a=-$\frac{5}{2}$或a=2.
∴当0≤a≤2时,f′(a)≤0,f(a)在[0,2]上是减函数.
∴当a=0时,f(a)取得最大值,即AF,EG所成角的余弦值最大,AF,EG所成角最小.
当a=0时,G与C重合.连结FC,则∠AFC为FG与平面AA1BB1所成的角.
∵BC=$\sqrt{2}$AC=2$\sqrt{2}$,AF=$\sqrt{5}$,CF=$\sqrt{B{C}^{2}+B{F}^{2}}$=3,
∴cos∠AFC=$\frac{AF}{CF}$=$\frac{\sqrt{5}}{3}$.
故答案为:$\frac{{\sqrt{5}}}{3}$.
点评 本题考查了空间角的计算,空间向量的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{10}$个单位长度 | B. | 向右平移$\frac{π}{10}$个单位长度 | ||
| C. | 向左平移$\frac{π}{5}$个单位长度 | D. | 向右平移$\frac{π}{5}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -4 | C. | $-\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
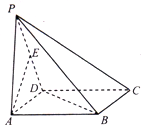 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com