
分析 由题意可得acosA-bcosB=0,利用正弦定理化边为角,得到sin2A=sin2B.再由A,B为三角形的两个内角,可得A=B或A+B=$\frac{π}{2}$,得到三角形为等腰三角形或直角三角形.
解答 解:由$|\begin{array}{l}{a}&{sin(\frac{π}{2}+B)}\\{b}&{cosA}\end{array}|$=0,得a•cosA-b$•sin(\frac{π}{2}+B)=0$,
即acosA-bcosB=0,
由正弦定理可得:sinAcosA-sinBcosB=0,
∴sin2A=sin2B.
∵A,B为三角形的两个内角,
∴2A=2B或2A+2B=π.
即A=B或A+B=$\frac{π}{2}$,
∴△ABC的形状为等腰三角形或直角三角形.
故答案为:等腰三角形或直角三角形.
点评 本题考查二阶矩阵的应用,考查了利用正弦定理判断三角形的形状,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
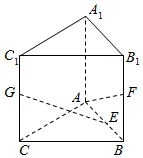 已知三棱柱ABC-A1B1C1,侧棱AA1⊥底面ABC,AB=AC=AA1=2,∠BAC=90°,E,F分别是AB,BB1的中点,G为CC1上动点,当AF,EG所成角最小时,FG与平面AA1BB1所成角的余弦值为$\frac{\sqrt{5}}{3}$.
已知三棱柱ABC-A1B1C1,侧棱AA1⊥底面ABC,AB=AC=AA1=2,∠BAC=90°,E,F分别是AB,BB1的中点,G为CC1上动点,当AF,EG所成角最小时,FG与平面AA1BB1所成角的余弦值为$\frac{\sqrt{5}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某校高二年级有10个班,1班62人,2班61人,3班62人,由此推测各班人数都超过60人 | |
| B. | 根据三角形的性质,可以推测空间四面体的性质 | |
| C. | 平行四边形对角线互相平分,矩形是平行四边形,所以矩形的对角线互相平分 | |
| D. | 在数列{an}中,a1=1,an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$,n∈N*,计算a2,a3,由此归纳出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com