练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
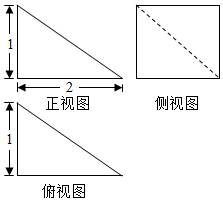
    14．某四棱锥的三视图如图所示，则该四棱锥的外接球的表面积是（　　）
    A．4πB．6πC．12πD．24π

    分析 据三视图知几何体是一个四棱锥，把四棱锥放在对应的长方体中，由长方体的体对角线是球的直径，求出外接球的半径，利用球体的表面积公式计算即可．

    解答 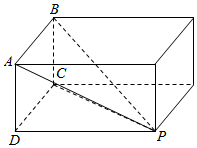解：如图：根据三视图知几何体是一个四棱锥P-ABCD
    且AD=1、PD=2、CD=1，
    ∴四棱锥P-ABCD的外接球也是此长方体的外接球，设半径为R，
    则2R=$\sqrt{{1}^{2}+{2}^{2}+{1}^{2}}$，解得R=$\frac{\sqrt{6}}{2}$，
    ∴该四棱锥的外接球的表面积S=$4π×（\frac{\sqrt{6}}{2}）^{2}=6π$，
    故选：B．

    点评 本题考查三视图求几何体的外接球的表面积，将几何体的外接球转化为对应长方体的外接球是解题的关键，考查空间想象能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．为了促进人口的均衡发展，我国从2016年1月1日起，全国统一实施全面放开两孩政策．为了解适龄国民对放开生育二胎政策的态度，某部门选取70后和80后年龄段的人作为调查对象，进行了问卷调查，其中，持“支持生二胎”、“不支持生二胎”和“保留意见”态度的人数如表所示：
    （1）在所有参与调查的人中，用分层抽样的方法抽取n个人，其中持“支持”态度的人共36人，求n的值；
    （2）在持“不支持”态度的人中，仍用分层抽样的方法抽取5人，并将其看成一个总体，从这5人中任意选取2人，求至少有1个80后的概率．
    支持保留不支持
    80后780420200
    70后120180300

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．为贯彻“咬文嚼字抓理解，突出重点抓记忆”的学习思想．某校从高一年级和高二年级各选取100名同学进行现学段基本概念知识竞赛．图（1）和图（2）分别是对高一年级和高二年级参加竞赛的学生成绩按[40，50），[50，60），[60，70），[70，80]分组，得到的频率分布直方图．

    （1）分别计算参加这次知识竞赛的两个年级学生的平均成绩；（注：统计方法中，同一组数据常用该组区间的中点值作为代表）
    （2）完成下面2×2列联表，并回答是否有99%的把握认为“两个年级学生现学段对基本知识的了解有差异”？
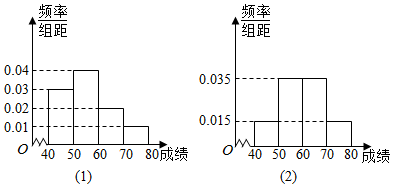
    成绩小于60分人数成绩不小于60分人数合计
    高一年级
    高二年级
    合计
    附：K2=$\frac{n（ad-bc）2}{（a+b）（c+d）（a+c）（b+d）}$．临界值表：
    P（K2≥k）0.100.050.010
    k2.7063.8416.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在△ABC中，边a、b、c所对角分别为A、B、C，若$|\begin{array}{l}{a}&{sin（\frac{π}{2}+B）}\\{b}&{cosA}\end{array}|$=0，则△ABC的形状为等腰三角形或直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=$\sqrt{3}$sin2x+cos2x-1（x∈R）；
    （1）写出函数f（x）的最小正周期和单调递增区间；
    （2）在△ABC中，角A、B、C所对的边分别是a、b、c，若f（B）=0，$\overrightarrow{BA}•\overrightarrow{BC}$=$\frac{3}{2}$，且a+c=4，试求b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，△ABC的外接圆半径为R，若C=$\frac{3π}{4}$，且sin（A+C）=$\frac{BC}{R}$•cos（A+B）．
    （1）证明：BC，AC，2BC成等比数列；
    （2）若△ABC的面积是1，求边AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=$\sqrt{3}$sinxcosx-cos2x-$\frac{1}{2}$，x∈R，则函数f（x）的最小值为-2，函数f（x）的递增区间为[$-\frac{π}{6}+kπ，\frac{π}{3}+kπ$]，k∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=-$\frac{1}{2}{x^2}$+4x-3lnx，则下列说法正确的是（　　）
    A．f（x）的单调递减区间为（1，3）B．x=3是函数f（x）的极小值点
    C．f（x）的单调递减区间为（0，1）∪（3，+∞）D．x=1是函数f（x）的极小值点

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

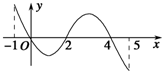    4．已知函数f（x）的定义域为[-1，5]，部分对应值如表．f（x）的导函数y=f′（x）的图象如图所示．
    x-1045
    f（x）1221
    下列关于函数f（x）的命题说法正确的是（　　）
    A．函数y=f（x）是周期函数
    B．当1＜a＜2时，函数y=f（x）-a有4个零点
    C．如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4
    D．函数f（x）在[0，2]上是减函数

    查看答案和解析>>

    同步练习册答案