
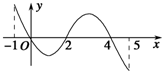
 已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 函数y=f(x)是周期函数 | |
| B. | 当1<a<2时,函数y=f(x)-a有4个零点 | |
| C. | 如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4 | |
| D. | 函数f(x)在[0,2]上是减函数 |
分析 根据函数的单调性和特殊值,可判断A的真假,
由f(x)=a,因为极小值f(2)未知,所以无法判断函数y=f(x)-a有几个零点,进而判断B的真假,
根据已知导函数的图象,及表中几个点的坐标,易分析出0≤t≤5,均能保证x∈[-1,t]时,f(x)的最大值是2,进而判断C的真假,
根据已知导函数的图象,易分析出f(x)在[0,2]上的单调性,可判断D的真假;
解答 解:由图象不能判断y出f(x)是否为周期函数,故A不正确;
由f(x)=a,因为极小值f(2)未知,所以无法判断函数y=f(x)-a有几个零点,所以B不正确;
由已知中y=f′(x)的图象,及表中数据可得当x=0或x=4时,函数取最大值2,若x∈[-1,t]时,f(x)的最大值是2,那么0≤t≤5,故t的最大值为5,即C不正确;
由已知中y=f′(x)的图象可得在[0,2]上f′(x)<0,即f(x)在[0,2]是减函数,即D正确;
故选:D.
点评 本题考查的知识点是命题的真假判断,利用导数研究函数的单调性,其中根据已知,分析出函数的大致形状,利用图象分析函数的性质是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com