
 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.分析 (Ⅰ)已知等式利用正弦定理化简,整理得到关系式,再利用余弦定理表示出cosB,将得出关系式代入求出cosB的值,确定出B的度数,由题意确定出sinC的值,再由b与sinB的值,利用正弦定理求出c的值,再利用余弦定理求出a的值即可;
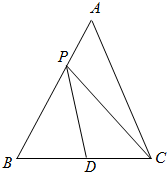
(Ⅱ)由A>$\frac{π}{6}$,知a=2,作C关于AB的对称点C′,连C′D,C′P,C′B,如图所示,由余弦定理求出C′D的长,利用两点之间线段最短即可确定出|CP|+|PD|的最小值.
解答 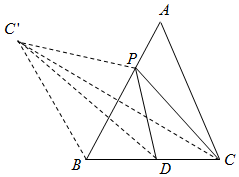 解:(Ⅰ)已知等式利用正弦定理化简得:$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-c}{a+b}$=$\frac{a-b}{c}$,
解:(Ⅰ)已知等式利用正弦定理化简得:$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-c}{a+b}$=$\frac{a-b}{c}$,
整理得:a2+c2-b2=ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
∵B为△ABC的内角,
∴B=$\frac{π}{3}$;
由cos2C=$\frac{1}{28}$,得到sinC=$\sqrt{\frac{27}{28}}$,
∵b=$\sqrt{7}$,sinB=$\frac{\sqrt{3}}{2}$,
由正弦定理得:$\frac{c}{sinC}$=$\frac{b}{sinB}$,即$\frac{c}{\sqrt{\frac{27}{28}}}$=$\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$,
解得:c=3,
由b2=a2+c2-ac,得7=a2+9-3a,即a2-3a+2=0,
解得:a=1或a=2;
(Ⅱ)由A>$\frac{π}{6}$,知a=2,作C关于AB的对称点C′,连C′D,C′P,C′B,
由余弦定理得:|C′D|2=|BD|2+|BC′|2+|BD|•|BC′|=12+22+2=7,
|CP|+|PD|=|C′P|+|PD|≥|C′D|=$\sqrt{7}$,
当C′,P,D共线时取等号,
则CP+PD的最小值为$\sqrt{7}$.
点评 此题考查了正弦、余弦定理,对称的性质,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调递减区间为(1,3) | B. | x=3是函数f(x)的极小值点 | ||
| C. | f(x)的单调递减区间为(0,1)∪(3,+∞) | D. | x=1是函数f(x)的极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
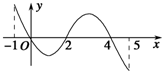 已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 函数y=f(x)是周期函数 | |
| B. | 当1<a<2时,函数y=f(x)-a有4个零点 | |
| C. | 如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4 | |
| D. | 函数f(x)在[0,2]上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8n}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{n}{4n+4}$ | D. | $\frac{n}{4n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com