
| A. | f(x)的单调递减区间为(1,3) | B. | x=3是函数f(x)的极小值点 | ||
| C. | f(x)的单调递减区间为(0,1)∪(3,+∞) | D. | x=1是函数f(x)的极小值点 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某校高二年级有10个班,1班62人,2班61人,3班62人,由此推测各班人数都超过60人 | |
| B. | 根据三角形的性质,可以推测空间四面体的性质 | |
| C. | 平行四边形对角线互相平分,矩形是平行四边形,所以矩形的对角线互相平分 | |
| D. | 在数列{an}中,a1=1,an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$,n∈N*,计算a2,a3,由此归纳出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{2}$ | B. | -$\frac{5\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{17}}{17}$ | D. | -$\frac{5\sqrt{17}}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
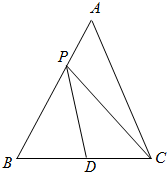 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com