
| A�� | ijУ�߶��꼶��10���࣬1��62�ˣ�2��61�ˣ�3��62�ˣ��ɴ��Ʋ��������������60�� | |
| B�� | ���������ε����ʣ������Ʋ�ռ������������ | |
| C�� | ƽ���ı��ζԽ�����ƽ�֣�������ƽ���ı��Σ����Ծ��εĶԽ�����ƽ�� | |
| D�� | ������{an}�У�a1=1��an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$��n��N*������a2��a3���ɴ˹��ɳ�{an}��ͨ�ʽ |
���� �����ѡ������֤��Bѡ���������������Aѡ���Dѡ����ڹ���������ֻ��Cѡ��������⣮
��� �⣺Aѡ�ijУ�߶��꼶��10���࣬1��62�ˣ�2��61�ˣ�3��62�ˣ��ɴ��Ʋ�������50�ˣ�Ҳ���ڹ���������
Bѡ��������ε����ʣ��Ʋ�ռ����������ʣ��������������
Cѡ��������ԵĴ�ǰ�ᣬСǰ�ᣬ���ۣ����ڵ��͵�������������������ʽ��
Dѡ�������{an}�У�a1=1��an+1=$\frac{{2{a_n}}}{{2+{a_n}}}$��n��N*���ɴ˹��ɳ�{an}��ͨ�ʽ�����ڹ���������
���ϣ���֪��ֻ��Cѡ��Ϊ����������
��ѡC��
���� ����Ϊ���������Ŀ��飬���ռ��������Ķ�����ص��ǽ������Ĺؼ����������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
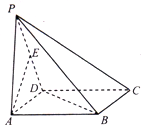 ������P-ABCD�У�����ABCDΪ�����Σ�PA�͵���ABCD��AB=AP��EΪ��PD���е�
������P-ABCD�У�����ABCDΪ�����Σ�PA�͵���ABCD��AB=AP��EΪ��PD���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x���ĵ����ݼ�����Ϊ��1��3�� | B�� | x=3�Ǻ���f��x���ļ�Сֵ�� | ||
| C�� | f��x���ĵ����ݼ�����Ϊ��0��1���ȣ�3��+�ޣ� | D�� | x=1�Ǻ���f��x���ļ�Сֵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
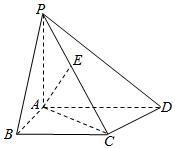 ��ͼ������P-ABCD�У�PA��ƽ��ABCD��AD��BC��PA=3��AD=4��AC=2$\sqrt{3}$����ADC=60�㣬EΪ�߶�PC��һ�㣬��$\overrightarrow{PE}$=��$\overrightarrow{PC}$��
��ͼ������P-ABCD�У�PA��ƽ��ABCD��AD��BC��PA=3��AD=4��AC=2$\sqrt{3}$����ADC=60�㣬EΪ�߶�PC��һ�㣬��$\overrightarrow{PE}$=��$\overrightarrow{PC}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com