
分析 利用三角恒等变换化简函数f(x)=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,
(Ⅰ)利用三角函数的图象与性质,即可求出f(x)的最小正周期与单调增区间;
(Ⅱ)根据$0≤x≤\frac{π}{4}$,求出$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{2π}{3}$,再根据正弦函数的图象与性质即可求出函数的最值.
解答 解:函数$f(x)=(\sqrt{3}cosx-sinx)sinx$
=$\sqrt{3}$sinxcosx-sin2x
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1-cos2x}{2}$
=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,x∈R;
(Ⅰ)f(x)的最小正周期为$T=\frac{2π}{2}=π$,
令$-\frac{π}{2}++2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ,k∈Z$,
解得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ$,
所以函数f(x)的单调增区间为
$[kπ-\frac{π}{3},kπ+\frac{π}{6}],k∈Z$;---(6分)
(Ⅱ)因为$0≤x≤\frac{π}{4}$,
所以$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{2π}{3}$,
所以$\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,
所以$0≤f(x)≤\frac{1}{2}$.
当且仅当x=0时 f(x)取最小值f(x)min=f(0)=0,
当且仅当$2x+\frac{π}{6}=\frac{π}{2}$,即$x=\frac{π}{6}$时f(x)取得最大值$f{(x)_{max}}=f(\frac{π}{6})=\frac{1}{2}$.---(12分)
点评 本题考查了三角函数的恒等变换的应用问题,也考查了三角函数的图象与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 80后 | 780 | 420 | 200 |
| 70后 | 120 | 180 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{10}$个单位长度 | B. | 向右平移$\frac{π}{10}$个单位长度 | ||
| C. | 向左平移$\frac{π}{5}$个单位长度 | D. | 向右平移$\frac{π}{5}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
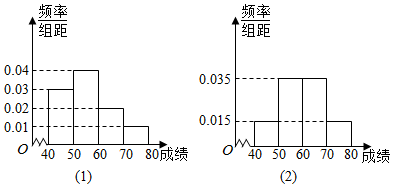
| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高一年级 | |||
| 高二年级 | |||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调递减区间为(1,3) | B. | x=3是函数f(x)的极小值点 | ||
| C. | f(x)的单调递减区间为(0,1)∪(3,+∞) | D. | x=1是函数f(x)的极小值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com