
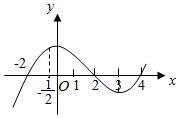 如果函数y=f(x)的导函数的图象如图所示,则函数y=f(x)的单调递增区间为(-2,2),(4,+∞).
如果函数y=f(x)的导函数的图象如图所示,则函数y=f(x)的单调递增区间为(-2,2),(4,+∞). 分析 导函数在某个区间上的函数值的符号是这样对应的,导数值为负,则函数在这个区间上是减函数,若导数为正,则函数在这个区间上是增函数,由此规则可以看到导数为正的区间,由图定出即可.
解答 解:由图象可以看出在(-2,2),(4,+∞)上,f′(x)≥0.
故数f(x)的单调递增区间为(-2,2),(4,+∞),
故答案为(-2,2),(4,+∞).
点评 本题考点是函数的单调性与单调区间,考查由导函数的图象判断函数的单调区间,这是导数的一个非常重要的运用,解答本题时有一个需要注意,那就是单调区间写成开区间还是闭区间的问题,一般要求是这样的如果在端点处函数有意义,一般将其写为闭区间,否则为开区间,如[2,+∞)的右端点,就只能写成开的形式.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2] | C. | [1,2] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com