
分析 (1)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)求出g(x)的导数,分离出参数a,根据函数的单调性求出函数的最小值,从而求出a的范围即可.
解答 解:(1)根据题意,f(x)=lnx-x,定义域为x∈(0,+∞)(1分)
$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$(2分),f'(x)>0⇒x<1,f'(x)<0⇒x>1(13分)
故在区间(0,1)函数单调递增,在区间(1,+∞)函数单调递减 (4分);
(2)$g(x)=lnx+ax+\frac{2}{x}$,$g'(x)=\frac{1}{x}+a-\frac{2}{x^2}$(5分)
函数(0,+∞)上单调递减,导数在(0,+∞)上g'(x)≤0恒成立(6分)
参变分离$\frac{1}{x}+a-\frac{2}{x^2}≤0⇒a≤\frac{2}{x^2}-\frac{1}{x}$(7分),
令$h(x)=\frac{2}{x^2}-\frac{1}{x}$,只需a≤h(x)min即可,
$h'(x)=-\frac{4}{x^3}+\frac{1}{x^2}=\frac{x-4}{x^3}$(9分)函数在区间(0,4)函数单调递减,在区间(4,+∞)函数单调递增 (10分),
∴$h{(4)_{min}}=\frac{2}{x^2}-\frac{1}{x}=-\frac{1}{8}$$a≤-\frac{1}{8}$(12分).
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,是一道中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 80后 | 780 | 420 | 200 |
| 70后 | 120 | 180 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
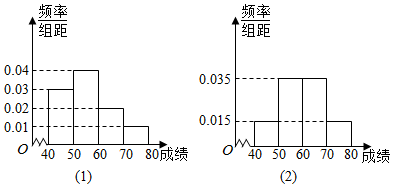
| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高一年级 | |||
| 高二年级 | |||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com