
| 支持 | 保留 | 不支持 | |
| 80后 | 780 | 420 | 200 |
| 70后 | 120 | 180 | 300 |
分析 (1)根据在抽样过程中每个个体被抽到的概率相等,写出比例式,使得比例相等,得到关于n的方程,解方程即可.
(2)由题意知本题是一个等可能事件的概率,本题解题的关键是列举出所有事件的事件数,再列举出满足条件的事件数,得到概率.
解答 解:(1)所有参与调查的人数为780+120+420+180+200+300=2000.
由分层抽样知$n=\frac{36}{900}×2000=80$…(5分)
(2)由分层抽样知抽取的5人中有2个80后(记为甲、乙),3个70后(记为A、B、C)
则从中任取两个,共有以下10种等可能的基本事件:
(甲,乙)、(甲,A)、(甲,B )、(甲,C)、(乙,A )、( 乙,B )、(乙,C )、(A,B)、(A,C)、(B,C),…(7分)
其中至少有1个80后的基本事件有(甲,乙)、(甲,A)、(甲,B)、(甲,C)、
(乙,A )、(乙,B )、(乙,C )共7种.…(9分)
故至少有1个80后的概率为$P=\frac{7}{10}$…(12分)
点评 本题主要考查分层抽样的定义和方法,古典概型及其概率计算公式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
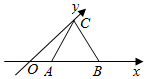
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com