
| A. | $\frac{1}{8n}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{n}{4n+4}$ | D. | $\frac{n}{4n+1}$ |
分析 函数g(x)=f(x)-knx 的零点个数可化为函数f(x)与y=knx的图象的交点的个数;作函数f(x)与y=knx的图象,结合图象可得y=knx的图象与y=$\sqrt{1-(x-2n-1)^{2}}$的图象相切,从而可得$\frac{1}{2}$$\frac{-2(x-2n-1)}{\sqrt{1-(x-2n-1)^{2}}}$=$\frac{1}{x}$$\sqrt{1-(x-2n-1)^{2}}$,从而解得kn=$\frac{1}{x}$$\sqrt{1-(x-2n-1)^{2}}$=$\frac{1}{2\sqrt{n(n+1)}}$,从而可得kn2=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),从而利用裂项求和法解得.
解答 解:函数g(x)=f(x)-knx 的零点个数可化为
函数f(x)与y=knx的图象的交点的个数;
作函数f(x)与y=knx的图象如下,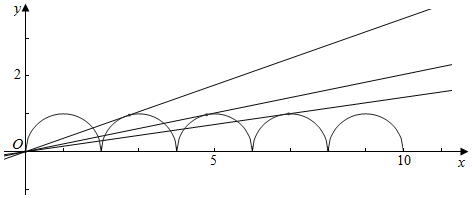 ,
,
∵关于x的函数g(x)=f(x)-knx 的零点个数恰好为2n+1个,
∴y=knx的图象与y=$\sqrt{1-(x-2n-1)^{2}}$的图象相切,
∴$\frac{1}{2}$$\frac{-2(x-2n-1)}{\sqrt{1-(x-2n-1)^{2}}}$=$\frac{1}{x}$$\sqrt{1-(x-2n-1)^{2}}$,
∴x=$\frac{4n(n+1)}{2n+1}$,
∴kn=$\frac{1}{x}$$\sqrt{1-(x-2n-1)^{2}}$
=$\frac{2n+1}{4n(n+1)}$$\sqrt{1-(\frac{4n(n+1)}{2n+1}-2n-1)^{2}}$
=$\frac{1}{2\sqrt{n(n+1)}}$,
∴kn2=$\frac{1}{4n(n+1)}$=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴k12+k22+…+kn2
=$\frac{1}{4}$(1-$\frac{1}{2}$)+$\frac{1}{4}$($\frac{1}{2}$-$\frac{1}{3}$)+$\frac{1}{4}$($\frac{1}{3}$-$\frac{1}{4}$)+…+$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$)
=$\frac{1}{4}$(1-$\frac{1}{n+1}$)=$\frac{n}{4(n+1)}$,
故选C.
点评 本题考查了导数的综合应用及数形结合的思想方法应用,同时考查了数列的性质与应用及裂项求和法的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{sinA-sinC}{sinA+sinB}$=$\frac{a-b}{c}$,b=$\sqrt{7}$,cos2C=$\frac{1}{28}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com