
【题目】【2016-2017学年辽宁省六校协作体高二下学期期初数学(理)】已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆
被圆![]() 所截得的弦
所截得的弦![]() 的长;
的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() 求直线
求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,且
,且![]() .
.
【解析】【试题分析】(1)依据题设先求圆的半径和方程,再运用弦心距、半弦长、半径之间的关系进行分析求解;(2)依据题设条件构造圆以![]() 的方程,再运用两圆的相交弦所在直线即为所求;(3)依据题设条件借助题设条件“
的方程,再运用两圆的相交弦所在直线即为所求;(3)依据题设条件借助题设条件“![]() 为钝角”建立不等式分析探求:
为钝角”建立不等式分析探求:
(1)由题意得:圆心![]() 到直线
到直线![]() 的距离为圆的半径,
的距离为圆的半径,
![]() ,所以圆
,所以圆![]() 的标准方程为:
的标准方程为: ![]()
所以圆心到直线![]() 的距离
的距离![]()
![]()
![]()
(2)因为点![]() ,所以
,所以![]() ,
,![]()
所以以![]() 点为圆心,线段
点为圆心,线段![]() 长为半径的圆
长为半径的圆![]() 方程:
方程: ![]() (1)
(1)
又圆![]() 方程为:
方程为: ![]() (2),由
(2),由![]() 得直线
得直线![]() 方程:
方程: ![]()
(3)设直线![]() 的方程为:
的方程为: ![]() 联立
联立![]() 得:
得: ![]() ,
,
设直线![]() 与圆的交点
与圆的交点![]() ,
,
由![]() ,得
,得![]() ,
, ![]() (3)
(3)
因为![]() 为钝角,所以
为钝角,所以![]() ,
,
即满足![]() ,且
,且![]() 与
与![]() 不是反向共线,
不是反向共线,
又![]() ,所以
,所以![]() (4)
(4)
由(3)(4)得![]() ,满足
,满足![]() ,即
,即![]() ,
,
当![]() 与
与![]() 反向共线时,直线
反向共线时,直线![]() 过原点,此时
过原点,此时![]() ,不满足题意,
,不满足题意,
故直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() ,且
,且![]()


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式 ![]() ; 函数
; 函数 ![]() (其中
(其中 ![]() ).
).
(1)若函数g(θ)的最大值为4,求m的值.
(2)若记集合M={m|恒有g(θ)>0},N={m|恒有f[g(θ)]<0},求M∩N.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() ,椭圆C2以C1的长轴为短轴,且与C1有
,椭圆C2以C1的长轴为短轴,且与C1有
相同的离心率.
(1)求椭圆Q的方程;
(2)设0为坐标原点,点A,B分别在椭圆C1和C2上,![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
(1)求这种“笼具”的体积;
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
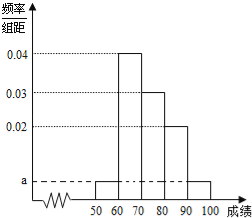
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系.已知点
轴的正半轴为极轴,建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为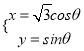 (
(![]() 为参数)
为参数)
(1)求点![]() 的直角坐标;化曲线
的直角坐标;化曲线![]() 的参数方程为普通方程;
的参数方程为普通方程;
(2)设![]() 为曲线
为曲线![]() 上一动点,以
上一动点,以![]() 为对角线的矩形
为对角线的矩形![]() 的一边垂直于极轴,求矩形
的一边垂直于极轴,求矩形![]() 周长的最小值,及此时
周长的最小值,及此时![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com