
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点![]() 作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
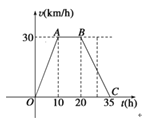
(1)当![]() 时,求s的值;
时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,对m,n∈R,恒有f(m+n)=f(m)·f(n)(f(m)≠0,f(n)≠0),且当x>0时,0<f(x)<1.
(1)求证f(0)=1;
(2)求证x∈R时,恒有f(x)>0;
(3)求证f(x)在R上是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③若扇形的周长为![]() ,圆心角为
,圆心角为![]() ,则该扇形的弧长为6cm;
,则该扇形的弧长为6cm;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
⑤函数![]() 的最小正周期是
的最小正周期是![]()
则上述结论中正确的是______(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2).
(如图2).

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个“蝴蝶形图案(阴影区域)”,其中![]() 是过抛物线
是过抛物线![]() 的两条互相垂直的弦(点
的两条互相垂直的弦(点![]() 在第二象限),且
在第二象限),且![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 轴上一点,
轴上一点,![]() ,其中
,其中![]() 为锐角
为锐角

(1)设线段![]() 的长为
的长为![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数
的函数
(2)求“蝴蝶形图案”面积的最小值,并指出取最小值时![]() 的大小
的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
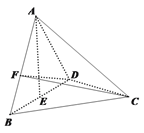
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com