
| 试销价格x(元) | 4 | 5 | 6 | 7 | a | 9 |
| 产品销量y(件) | b | 84 | 83 | 80 | 75 | 68 |
分析 (1)由变量x,y具有线性负相关关系,知甲是错误的,求出$\overline x=6.5,\overline y=80$,满足方程y=-4x+106,从而乙是正确的,由此能求出a,b.
(2)由计算可得“理想数据”有3个,从检测数据中随机抽取2个,共有15种不同的情形,这两个检测数据均为“理想数据”有3种情形,由此能求出这两个检验数据均为“理想数据”的概率.
解答 解:(1)∵变量x,y具有线性负相关关系,
∴甲是错误的.(2分)
又∵$\sum_{i=1}^6{x_i}=39,\sum_{i=1}^6{y_i}=480$,∴$\overline x=6.5,\overline y=80$,
满足方程y=-4x+106,故乙是正确的.(4分)
由$\sum_{i=1}^6{x_i}=39,\sum_{i=1}^6{y_i}=480$,得a=8,b=90.(6分)
(2)由计算可得“理想数据”有3个,
即(4,90),(6,83),(8,75).(8分)
从检测数据中随机抽取2个,共有15种不同的情形,
其中这两个检测数据均为“理想数据”有3种情形.(10分)
故所求概率为$P=\frac{3}{15}=\frac{1}{5}$.(12分)
点评 本题考查实数值的求法,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或22 | B. | 22 | C. | 2 | D. | 7或17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
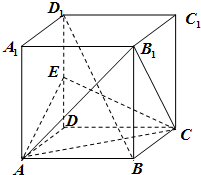 如图,在正四棱柱ABCD-A1B1C1D1中,E为DD1的中点,求证:
如图,在正四棱柱ABCD-A1B1C1D1中,E为DD1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (2,+∞) | C. | (0,2) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com