
分析 利用对数恒等式,以及函数的奇偶性的性质,求得结果.
解答 解:函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=($\frac{1}{2}$)x,
则f(log2$\frac{1}{3}$)=f(${log}_{\frac{1}{2}}3$)=-f(-${log}_{\frac{1}{2}}3$)=-f(${log}_{\frac{1}{2}}\frac{1}{3}$)=-${(\frac{1}{2})}^{{log}_{\frac{1}{2}}\frac{1}{3}}$=-$\frac{1}{3}$.
由于当x>0时,f(x)=($\frac{1}{2}$)x,∴f(x)∈(0,1),
再根据f(x)为奇函数,可得当x<0时,f(x)∈(-1,0).
又f(0)=0,故函数f(x)的值域为(-1,1),
故答案为:-$\frac{1}{3}$;(-1,1).
点评 本题主要考查对数恒等式,函数的奇偶性的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
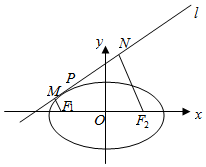 如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.
如图,在平面直角坐标系xOy中,直线l与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相切于点P,过椭圆的左、右焦点F1,F2分别作F1M,F2N重直于直线l于M,N,记μ=$\frac{{N{F_2}}}{{M{F_1}}}$,当P为左顶点时,μ=9,且当μ=1时,四边形MF1F2N的周长为22.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$](k∈Z) | ||
| C. | [$\frac{2kπ}{3}$-$\frac{π}{18}$,$\frac{2kπ}{3}$+$\frac{5π}{18}$](k∈Z) | D. | [$\frac{2kπ}{3}$-$\frac{7π}{18}$,$\frac{2kπ}{3}$-$\frac{π}{18}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com