
分析 两角和与差的余弦函数公式,三角形内角和定理化简已知等式可得2sinAsinB=2sin2C,结合正弦定理得ab=c2,又b2=a2+ab,可得b2=a2+c2,利用勾股定理即可证明.
解答 证明:∵cos(A-B)=cosAcosB+sinAsinB,cosC=-cos(A+B)=-cosAcosB+sinAsinB,
∴cos(A-B)+cosC=2sinAsinB,
又∵cos(A-B)+cosC=1-cos2C=2sin2C,
∴2sinAsinB=2sin2C,结合正弦定理得ab=c2,
∵b2=a(a+b)=a2+ab,
∴b2=a2+c2,可得△ABC是以B为直角的直角三角形.
点评 本题主要考查了两角和与差的余弦函数公式,三角形内角和定理,正弦定理,勾股定理在解三角形中的应用,考查了转化思想,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
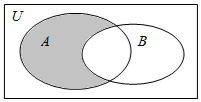 设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )
设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
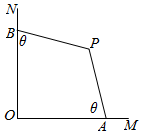 某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.
某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (2)
(2) (3)
(3)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a<-3或a>1} | B. | {a|a>1} | C. | {a|-3<x<1} | D. | {a|a<-3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com