
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 有一个宽为
有一个宽为![]() 的通道.给出下列函数:①
的通道.给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在区间
.其中在区间![]() 上通道宽度为1的函数由__________ (写出所有正确的序号).
上通道宽度为1的函数由__________ (写出所有正确的序号).
【答案】①②③.
【解析】
分析:对于①,求出函数的值域,判断即可;对于②,从函数图象入手,寻找符合条件的直线即可;对于③,利用导数研究函数的单调性,即可得其值域,判断即可;对于④,求出函数的值域,并根据导数的几何意义求出函数的切线方程,从而可判断.
详解:对于①,![]() ,当
,当![]() 时,
时,![]() ,故在
,故在![]() 上有一个宽度为1的通道,两条直线可取
上有一个宽度为1的通道,两条直线可取![]() ,
,![]() ;
;
对于②,![]() ,当
,当![]() 时,
时,![]() 表示的是双曲线
表示的是双曲线![]() 在第一象限的部分,双曲线的渐近线为
在第一象限的部分,双曲线的渐近线为![]() ,故函数
,故函数![]() 满足
满足![]() ,满足在
,满足在![]() 上有一个宽度为1的通道;
上有一个宽度为1的通道;
对于③,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,则
,则![]() ,且
,且![]() 在
在![]() 上的值域为
上的值域为![]() ,满足
,满足![]() ,故该函数满足在
,故该函数满足在![]() 上有一个宽度为1的通道;
上有一个宽度为1的通道;
对于④,![]() ,
,![]() ,
,![]() 与
与![]() 之间的距离为
之间的距离为![]() ,又因为
,又因为![]() ,则
,则![]() 为增函数,设
为增函数,设![]() 的切点为
的切点为![]() ,则
,则![]() ,解得
,解得![]() ,则与
,则与![]() 平行的切线为:
平行的切线为:![]() ,即
,即![]() ,
,![]() ,因为
,因为![]() 与
与![]() 相切,故不存在两条直线.
相切,故不存在两条直线.
故答案为①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,水平的广场上有一盏路灯挂在高![]() 的电线杆顶上,记电线杆的底部为点
的电线杆顶上,记电线杆的底部为点![]() .把路灯看作一个点光源,身高
.把路灯看作一个点光源,身高![]() 的女孩站在离点
的女孩站在离点![]() 的点
的点![]() 处,回答下面的问题.
处,回答下面的问题.

(1)若女孩以![]() 为半径绕着电线杆走一个圆圈,人影扫过的是什么图形,求这个图形的面积;
为半径绕着电线杆走一个圆圈,人影扫过的是什么图形,求这个图形的面积;
(2)若女孩向点![]() 前行
前行![]() 到达点
到达点![]() ,然后从点
,然后从点![]() 出发沿着以
出发沿着以![]() 为对角线的正方形走一圈,画出女孩走一圈时头顶影子的轨迹,说明轨迹的形状.
为对角线的正方形走一圈,画出女孩走一圈时头顶影子的轨迹,说明轨迹的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(![]() 个月)和市场占有率(
个月)和市场占有率(![]() )的几组相关对应数据:
)的几组相关对应数据:
| 1 | 2 | 3 | 4 | 5 |
| 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过![]() (精确到月).
(精确到月).
查看答案和解析>>
科目:高中数学 来源: 题型:
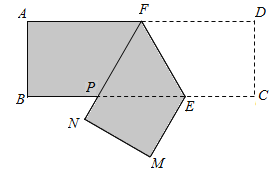
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() ,
,![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() ,
,![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ,再沿直线
,再沿直线![]() 裁剪.
裁剪.
(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分,设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)![]() 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
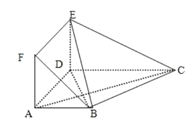
【题目】在多面体![]() 中,底面
中,底面![]() 是梯形,四边形
是梯形,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,
,![]() .
.![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,试问在线段
,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,试指出点
,若存在,试指出点![]() 的位置;若不存在,说明理由?
的位置;若不存在,说明理由?
(3)在(2)的条件下,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新鲜的荔枝很好吃,但摘下后容易变黑,影响卖相。某超市计划每年六月从精准扶贫户中订购荔枝,每天进货量相同且每公斤20元,当日18时前售价为每公斤24元,18时后以每公斤16元的价格销售完毕。根据往年情况,每天的荔枝需求量与当天平均气温有关,如下表表示:
平均气温t(摄氏度) |
|
|
|
|
需求量n(公斤) | 50 | 100 | 200 | 300 |
为了确定今年6月1日6月30日的日购数量,统计了前三年六月各天的平均气温,得到如下的频数分布表:
平均气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)假设该超市在以往三年内的六月每天进货100公斤,求荔枝为超市带来的日平均利润(结果取整数).
(2)若今年该超市进货量为200公斤,以记录的各需求量的频率作为相应的概率,求当天超市不亏损的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com