
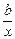 |≥2
|≥2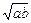 ;
;科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
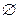 ,则不等式f(x)·g(x)>0的解集为
,则不等式f(x)·g(x)>0的解集为| A.{x|1≤x<2} | B.R |
C.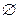 | D.{x|x<1或x≥2} |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
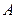 、
、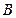 两种型号的车厢共50节运送这批货物.已知35 t甲种货物和15 t乙种货物可装满一节
两种型号的车厢共50节运送这批货物.已知35 t甲种货物和15 t乙种货物可装满一节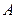 型货厢;25 t甲种货物和35 t乙种货物可装满一节
型货厢;25 t甲种货物和35 t乙种货物可装满一节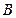 型货物,据此安排
型货物,据此安排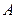 、
、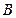 两种货厢的节数,共有几种方案?若每节
两种货厢的节数,共有几种方案?若每节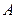 型货厢的运费是0.5万元,每节
型货厢的运费是0.5万元,每节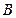 型货物的运费是0.8万元,哪种方案的运费最少?
型货物的运费是0.8万元,哪种方案的运费最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
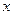 (辆)与创造的价值
(辆)与创造的价值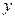 (元)之间有如下的关系:
(元)之间有如下的关系: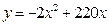 .若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?
.若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com