
| A. | $1\frac{61}{66}$升 | B. | 2升 | C. | $2\frac{3}{22}$升 | D. | 3升 |
分析 利用已知条件列出方程组,利用等差数列求出首项与公差,然后求解即可.
解答 解:设竹九节由上往下的容量分别为a1,a2,a3,a4,a5,a6,a7,a8,a9,
由题意可知:$\left\{\begin{array}{l}{a_1}+{a_2}+{a_3}+{a_4}=3\\{a_7}+{a_8}+{a_9}=4\end{array}\right.$$⇒\left\{\begin{array}{l}{a_1}=\frac{13}{22}\\ d=\frac{7}{66}\end{array}\right.$,
所以问题中的中间两节容量和为a5+a6=2a1+9d=$\frac{47}{22}$
=$2\frac{3}{22}$.
故选:C.
点评 本题考查等差数列的应用,判断数列是等差数列是解题的关键,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
| 广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
| 销售收入y | 16 | 23 | 25 | 26 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
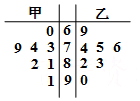 某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | 1>($\frac{1}{2}$)b>($\frac{1}{2}$)a | C. | $\frac{b}{a}$+$\frac{a}{b}$<2 | D. | aeb>bea |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | 1 | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com