
分析 (1)利用极坐标与直角坐标的转化方法,求曲线C的普通方程,即可指出它是什么曲线.
(2)当直线E与圆心连线垂直时弦长最小,利用勾股定理可得结论.
解答 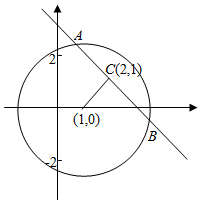 解:(1)∵曲线C:ρ2-2ρcosθ-8=0,
解:(1)∵曲线C:ρ2-2ρcosθ-8=0,
∴x+y-2x-8=0,
∴(x-1)2+y2=9,
表示圆心(1,0)半径为3的圆;
(2)曲线E:$\left\{\begin{array}{l}{x=t+2}\\{y=kt+1}\end{array}\right.$消去参数得y-1=k(x-2)m是一条恒过定点(2,1)的直线(但不包括x=2),当直线E与圆心连线垂直时弦长最小,
设圆心到直线E的距离为d,则d=$\sqrt{2}$,所以弦长的最小值=2$\sqrt{9-2}$=2$\sqrt{7}$
点评 本题考查极坐标与直角坐标的转化,考查直线过定点,考查直线与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1\frac{61}{66}$升 | B. | 2升 | C. | $2\frac{3}{22}$升 | D. | 3升 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
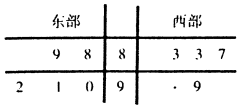 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{6},5}]$ | B. | [1,5] | C. | $[{\frac{1}{4},5}]$ | D. | [0,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com