
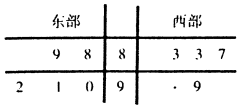
 ijʡ����̨Ϊ�˽��ʡ����һ���������Ŀ�������������鶫��������5�����У��õ��ۿ��ý�Ŀ����������λ��ǧ�ˣ����¾�Ҷͼ��ʾ��
ijʡ����̨Ϊ�˽��ʡ����һ���������Ŀ�������������鶫��������5�����У��õ��ۿ��ý�Ŀ����������λ��ǧ�ˣ����¾�Ҷͼ��ʾ��| ����x���꣩ | 20 | 30 | 40 | 50 |
| �ܾ�ѧϰ����֪ʶʱ��y��Сʱ�� | 2.5 | 3 | 4 | 4.5 |
���� ��1����������¼��ĸ���������������ʣ�
��2������ع�ϵ�����ɵûع鷽�̣���Ԥ������Ϊ55������ܾ�ѧϰ����֪ʶʱ�䣮
��� �⣺��1���豻���������Ϊa����a��10�������
��88+89+90+91+92��83+83+97+90+a+99����a��8��
�ණ�������йۿ��ý�Ŀ����ƽ�������������������йۿ��ý�Ŀ����ƽ����������8�������
�����Ϊ$\frac{8}{10}$=$\frac{4}{5}$��
��2���ɱ������ݵ�$\overline{x}$=35��$\overline{y}$=3.5��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$=$\frac{525-10��35��3.5}{5400-10��3{5}^{2}}$=$\frac{7}{100}$��$\stackrel{��}{a}$=$\frac{21}{20}$
��$\stackrel{��}{y}$=$\frac{7}{100}$x+$\frac{21}{20}$��
x=55ʱ��$\stackrel{��}{y}$=4.9Сʱ��
��Ԥ������Ϊ55�����ܾ�ѧϰ����֪ʶʱ��Ϊ4.9Сʱ��
���� ���⿼��ŵ�����ʵļ��㣬��������Լ���֪ʶ�����ã������е��⣮


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2��b2 | B�� | 1����$\frac{1}{2}$��b����$\frac{1}{2}$��a | C�� | $\frac{b}{a}$+$\frac{a}{b}$��2 | D�� | aeb��bea |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
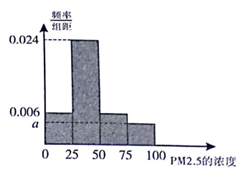 ���ݹ��һ����������ġ������������������涨��������PM2.5����ƽ��Ũ�Ȳ��ó���35��/�����ף�PM2.5��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��30��PM2.5��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����30��IJ���������Ƴ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���ݹ��һ����������ġ������������������涨��������PM2.5����ƽ��Ũ�Ȳ��ó���35��/�����ף�PM2.5��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��30��PM2.5��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����30��IJ���������Ƴ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{5}$ | B�� | $\sqrt{5}$ | C�� | 1 | D�� | $\frac{2\sqrt{5}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -80 | B�� | -16 | C�� | 80 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com