练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．二项式${（{{x^2}-\frac{2}{{\sqrt{x}}}}）^5}$展开式的常数项为（　　）
    A．-80B．-16C．80D．16

    分析 利用通项公式即可得出．

    解答 解：二项式${（{{x^2}-\frac{2}{{\sqrt{x}}}}）^5}$展开式的通项公式：Tr+1=${∁}_{5}^{r}$（x2）5-r$（-\frac{2}{\sqrt{x}}）^{r}$=（-2）r${∁}_{5}^{r}$${x}^{10-\frac{5r}{2}}$．
    令10-$\frac{5r}{2}$=0，解得r=4．
    ∴常数项=（-2）4${∁}_{5}^{4}$=80．
    故选：C．

    点评 本题考查了二项式定理的应用、方程的解法，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=2sinx•sin（x+$\frac{π}{3}$）．
    （Ⅰ）求函数f（x）的单调递增区间；
    （Ⅱ）锐角△ABC的角A，B，C所对边分别是a，b，c，角A的平分线交BC于D，直线x=A是函数f（x）图象的一条对称轴，AD=$\sqrt{2}$BD=2，求边a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

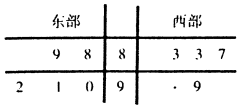    9．某省电视台为了解该省卫视一档成语类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数（单位：千人）如下茎叶图所示：
    其中一个数字被污损．
    （1）求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率．
    （2）随着节目的播出，极大激发了观众对成语知识的学习积累的热情，从中获益匪浅．现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y（单位：小时）与年龄x（单位：岁），并制作了对照表（如表所示）
    年龄x（岁）20304050
    周均学习成语知识时间y（小时）2.5344.5
    由表中数据，试求线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并预测年龄为55岁观众周均学习成语知识时间．
    参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|，且（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则$\overrightarrow{a}$，$\overrightarrow{b}$的夹角等于（　　）
    A．$\frac{2π}{3}$B．$\frac{5π}{6}$C．$\frac{π}{3}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知实数x，y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$，则$\frac{y+1}{x+1}$的取值范围是（　　）
    A．$[{-\frac{1}{6}，5}]$B．[1，5]C．$[{\frac{1}{4}，5}]$D．[0，5]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

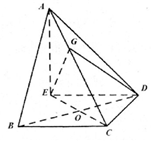    3．如图，在三棱锥A-BCD中，∠ABC=∠BCD=∠CDA=90°，AC=6$\sqrt{3}$，BC=CD=6，E点在平面BCD内，EC=BD，EC⊥BD．
    （Ⅰ）求证：AE⊥平面BCDE；
    （Ⅱ）设点G在棱AC上，若二面角C-EG-D的余弦值为$\frac{{\sqrt{10}}}{5}$，试求$\frac{CG}{GA}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数$f（x）=（x-\frac{1}{x}）sinx$（-π≤x≤π且x≠0）的图象是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知△ABC中，角A，B，C所对的边依次为a，b，c，其中b=2．
    （Ⅰ）若asin2B=$\sqrt{3}$bsinA，求B；
    （Ⅱ）若a，b，c成等比数列，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

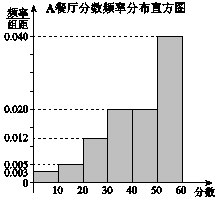    8．某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
    B餐厅分数频数分布表
    分数区间频数
    [0，10）2
    [10，20）3
    [20，30）5
    [30，40）15
    [40，50）40
    [50，60]35
    （Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
    （Ⅱ）从对B餐厅评分在[0，20）范围内的人中随机选出2人，求2人中恰有1人评分在[0，10）范围内的概率；
    （Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

    查看答案和解析>>

    同步练习册答案