
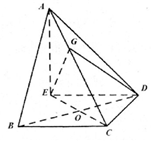
 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.分析 (Ⅰ)连接BE,设BD交CE于O,只需证明CD⊥AE,BC⊥AE,BC∩CD=C,即可得所以AE⊥平面BCDE
(Ⅱ)由(Ⅰ)的证明过程知BCDE为正方形,如图建立坐标系,
则:E(0,0,0),D(0,6,0),A(0,0,6),B(6,0,0),C(6,6,0)
设$\frac{CG}{GA}=t$(t>0),G(x,y,z)
由$\overrightarrow{CG}=t\overrightarrow{GA}$可得$G({\frac{6}{1+t},\frac{6}{1+t},\frac{6t}{1+t}})$,则$\overrightarrow{ED}=({0,6,0})$,$\overrightarrow{EG}=({\frac{6}{1+t},\frac{6}{1+t},\frac{6t}{1+t}})$
易知平面CEG的一个法向量为$\overrightarrow{DB}=({6,-6,0})$,求出平面DEG的一个法向量为$\overrightarrow n=({{x_0},{y_0},{z_0}})$.
利用向量的夹角公式求解.
解答 解:(Ⅰ)证明:连接BE,设BD交CE于O,
因为△BCD是等腰直角三角形CO⊥BD,所以$CO=\frac{1}{2}BD$,又EC=BD,所以O是BD和CE的中点
已知EC⊥BD,所以四边形BCDE是正方形
则CD⊥ED,又CD⊥AD,AD∩CD=D
所以CD⊥平面ADE,CD⊥AE
同理BC⊥AE,BC∩CD=C
所以AE⊥平面BCDE;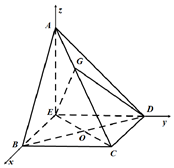
(Ⅱ)由(Ⅰ)的证明过程知BCDE为正方形,如图建立坐标系,
则:E(0,0,0),D(0,6,0),A(0,0,6),B(6,0,0),C(6,6,0)
设$\frac{CG}{GA}=t$(t>0),G(x,y,z)
由$\overrightarrow{CG}=t\overrightarrow{GA}$可得$G({\frac{6}{1+t},\frac{6}{1+t},\frac{6t}{1+t}})$
则$\overrightarrow{ED}=({0,6,0})$,$\overrightarrow{EG}=({\frac{6}{1+t},\frac{6}{1+t},\frac{6t}{1+t}})$
易知平面CEG的一个法向量为$\overrightarrow{DB}=({6,-6,0})$
设平面DEG的一个法向量为$\overrightarrow n=({{x_0},{y_0},{z_0}})$
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{ED}=0\\ \overrightarrow n•\overrightarrow{EG}=0\end{array}\right.$得$\left\{\begin{array}{l}6{y_0}=0\\ \frac{6}{1+t}{x_0}+\frac{6}{1+t}{y_0}+\frac{6t}{1+t}{z_0}=0\end{array}\right.$
令x0=1得${z_0}=-\frac{1}{t}$,$\overrightarrow n=({1,0,-\frac{1}{t}})$
所以$\frac{{\overrightarrow{DB}•\overrightarrow n}}{{|{\overrightarrow{DB}}|•|{\overrightarrow n}|}}=\frac{{\sqrt{10}}}{5}$,$\frac{6}{{6\sqrt{2}•\sqrt{1+\frac{1}{t^2}}}}=\frac{{\sqrt{10}}}{5}$
解得t=2,所以$\frac{CG}{GA}=2$.
点评 本题考查了空间线面垂直的判定,向量法求二面角,属于中档题.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
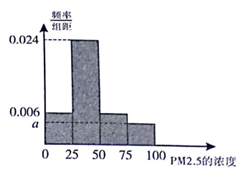 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
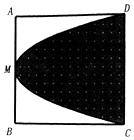 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -80 | B. | -16 | C. | 80 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,1) | C. | (1,+∞) | D. | (-∞,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com