练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设i是虚数单位，若$z=\frac{2}{-1+i}$，则复数z的虚部是（　　）
    A．1B．iC．-1D．-i

    分析 直接由复数代数形式的乘除运算化简复数z得答案．

    解答 解：$z=\frac{2}{-1+i}$=$\frac{2（-1-i）}{（-1+i）（-1-i）}=\frac{-2-2i}{2}=-1-i$，
    则复数z的虚部是：-1．
    故选：C．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

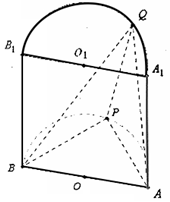    2．如图半圆柱OO1的底面半径和高都是1，面ABB1A1是它的轴截面（过上下底面圆心连线OO1的平面），Q，P分别是上下底面半圆周上一点．
    （1）证明：三棱锥Q-ABP体积VQ-ABP≤$\frac{1}{3}$，并指出P和Q满足什么条件时有AP⊥BQ
    （2）求二面角P-AB-Q平面角的取值范围，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

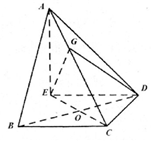    3．如图，在三棱锥A-BCD中，∠ABC=∠BCD=∠CDA=90°，AC=6$\sqrt{3}$，BC=CD=6，E点在平面BCD内，EC=BD，EC⊥BD．
    （Ⅰ）求证：AE⊥平面BCDE；
    （Ⅱ）设点G在棱AC上，若二面角C-EG-D的余弦值为$\frac{{\sqrt{10}}}{5}$，试求$\frac{CG}{GA}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．为调查我市居民对“文明出行”相关规定的了解情况，某媒体随机选取了30名行人进行问卷调查，将他们的年龄整理后分组，制成下表：
    年龄（岁）（12，22]（22，32]（32，42]（42，52]（52，62]（62，72]
    频数m3754n
    己知从中任选一人，年龄在（12，22]的频率为0.3
    （I）求m，n的值；
    （II）通过问卷得知，参与调查的52岁以上的两个组中，了解相关规定的人各占$\frac{1}{2}$．现从这两个组中任选2人，求选取的2人都了解相关规定的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知△ABC中，角A，B，C所对的边依次为a，b，c，其中b=2．
    （Ⅰ）若asin2B=$\sqrt{3}$bsinA，求B；
    （Ⅱ）若a，b，c成等比数列，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

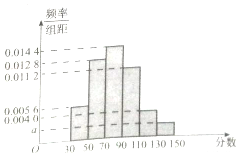    17．某市高二年级学生进行数学竞赛，竞赛分为初赛和决赛，规定成绩在110分及110分以上的学生进入决赛，110分以下的学生则被淘汰，现随机抽取500名学生的初赛成绩按[30，50），[50，70），[70，90），[90，110），[110，130），[130，150]做成频率副本直方图，如图所示：（假设成绩在频率分布直方图中各段是均匀分布的）
    （1）求这500名学生中进入决赛的人数，及进入决赛学生的平均分（结果保留一位小数）；
    （2）用频率估计概率，在全市进入决赛的学生中选取三人，其中成绩在[130，150]的学生数为X，试写出X的分布列，并求出X的数学期望及方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

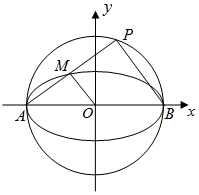    4．已知椭圆C的中心在原点，焦点在x轴上，离心率$e=\frac{{\sqrt{3}}}{2}$．且经过点（0，1），C与x轴交于A，B两点，以AB为直径的圆记为C1，P是C1上的异于A，B的点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若PA与椭圆C交于点M，且满足|PB|=2|OM|，求点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

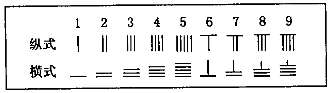
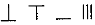    1．中国有个名句“运筹帷幄之中，决胜千里之外”．其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如表：

    表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推，例如6613用算筹表示就是：，则5288用算筹式可表示为．

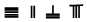    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{a{x}^{2}}{{e}^{x}}$，直线y=$\frac{1}{e}$x为曲线y=f（x）的切线．
    （1）求实数a的值；
    （2）用min{m，n}表示m，n中的较小值，设函数g（x）=min{f（x），x-$\frac{1}{x}$}（x＞0），若函数h（x）=g（x）-cx2为增函数，求实数c的取值范围．

    查看答案和解析>>

    同步练习册答案